Эмпирическая функция распределения
| Случайность – это старейшая знать мира, которая избавлена … от рабства под игом цели. Ф. Ницше. "Так говорил Заратустра". |
Методы обработки ЭД опираются на базовые понятия теории вероятностей и математической статистики. К их числу относятся понятия генеральной совокупности, выборки, эмпирической функции распределения [3, 5].
Под генеральной совокупностью понимают все возможные значения параметра, которые могут быть зарегистрированы в ходе неограниченного по времени наблюдения за объектом. Такая совокупность состоит из бесконечного множества элементов. В результате наблюдения за объектом формируется ограниченная по объему совокупность значений параметра x1, x2, …, xn. С формальной точки зрения такие данные представляют собой выборкуиз генеральной совокупности.
Будем считать, что выборка содержит полные наработки до системных событий (цензурирование отсутствует). Наблюдаемые значения xiназывают вариантами, а их количество – объемом выборки n. Для того чтобы по результатам наблюдения можно было делать какие-либо выводы, выборка должна быть репрезентативной (представительной), т. е. правильно представлять пропорции генеральной совокупности. Это требование выполняется, если объем выборки достаточно велик, а каждый элемент генеральной совокупности имеет одинаковую вероятность попасть в выборку.
Пусть в полученной выборке значение x1 параметра наблюдалось n1 раз, значение x2 – n2 раз, значение xk – nk раз, n1+n2+ …+nk=n.
Совокупность значений, записанных в порядке их возрастания, называют вариационным рядом, величины ni– частотами, а их отношения к объему выборки ni=ni/n – относительными частотами (частостями). Очевидно, что сумма относительных частот равна единице.
Под распределением понимают соответствие между наблюдаемыми вариантами и их частотами или частостями. Пусть nx – количество наблюдений, при которых случайные значения параметра Х меньше x. Частость события X<x равна nx/n . Это отношение является функцией от x и от объема выборки: Fn(x)=nx /n. Величина Fn(x) обладает всеми свойствами функции:
распределения: Fn(x) неубывающая функция, ее значения принадлежат отрезку [0 – 1];
если x1 – наименьшее значение параметра, а xk – наибольшее, то Fn(x)=0, когда x<x1 , и Fп(xk)=1, когда x>=xk.
Функция Fn(x) определяется по ЭД, поэтому ее называют эмпирической функцией распределения. В отличие от эмпирической функции Fn(x) функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения, она характеризует не частость, а вероятность события X<x. Из теоремы Бернулли вытекает, что частость Fn(x) стремится по вероятности к вероятности F(x) при неограниченном увеличении n. Следовательно, при большом объеме наблюдений теоретическую функцию распределения F(x) можно заменить эмпирической функцией Fn(x).
График эмпирической функции Fn(x) представляет собой ломаную линию. В промежутках между соседними членами вариационного ряда Fn(x) сохраняет постоянное значение. При переходе через точки оси x, равные членам выборки, Fn(x) претерпевает разрыв, скачком возрастая на величину 1/n, а при совпадении l наблюдений – на l/n.
Пример 2.1. Построить вариационный ряд и график эмпирической функции распределения по результатам наблюдений, табл. 2.1.
Таблица 2.1
| i | ||||||
| xi |
Решение. Построим вариационный ряд, упорядочив по возрастанию значения варианты, табл. 2.2.
Таблица 2.2
| i | ||||||
| xi |
Искомая эмпирическая функция, рис. 2.1:

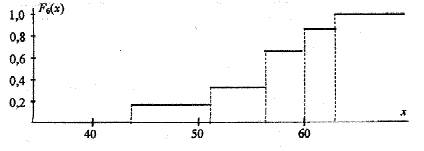
Рис. 2.1. Эмпирическая функция распределения
При большом объеме выборки (понятие «большой объем» зависит от целей и методов обработки, в данном случае будем считать п большим, если n>40) в целях удобства обработки и хранения сведений прибегают к группированию ЭД в интервалы. Количество интервалов следует выбрать так, чтобы в необходимой мере отразилось разнообразие значений параметра в совокупности и в то же время закономерность распределения не искажалась случайными колебаниями частот по отдельным разрядам. Существуют нестрогие рекомендации по выбору количества y и размера h таких интервалов, в частности:
в каждом интервале должно находиться не менее 5 – 7 элементов. В крайних разрядах допустимо всего два элемента;
количество интервалов не должно быть очень большим или очень маленьким. Минимальное значение y должно быть не менее 6 – 7. При объеме выборки, не превышающем несколько сотен элементов, величину y задают в пределах от 10 до 20. Для очень большого объема выборки (n>1000) количество интервалов может превышать указанные значения. Некоторые исследователи рекомендуют пользоваться соотношением y=1,441*ln(n)+1;
при относительно небольшой неравномерности длины интервалов удобно выбирать одинаковыми и равными величине
h=(xmax – xmin)/y,
где xmax – максимальное и xmin – минимальное значение параметра. При существенной неравномерности закона распределения длины интервалов можно задавать меньшего размера в области быстрого изменения плотности распределения;
при значительной неравномерности лучше в каждый разряд назначать примерно одинаковое количество элементов выборки. Тогда длина конкретного интервала будет определять крайними значениями элементов выборки, сгруппироваными в этот интервал, т.е. будет различна для разных интервалов (в этом случае при построении гистограммы нормировка по длине интервала обязательна - в противном случае высота каждого элемента гистограммы будет одинакова).
Группирование результатов наблюдений по интервалам предусматривает: определение размаха изменений параметра х; выбор количества интервалов и их величины; подсчет для каждого i-го интервала [xi–xi+1] частоты ni или относительной частоты (частости ni) попадания варианты в интервал. В результате формируется представление ЭД в виде интервального или статистического ряда.
Графически статистический ряд отображают в виде гистограммы, полигона и ступенчатой линии. Часто гистограмму представляют как фигуру, состоящую из прямоугольников, основаниями которых служат интервалы длиною h, а высоты равны соответствующей частости. Однако такой подход неточен. Высоту i-го прямоугольника zi следует выбрать равной ni/(nh). Такую гистограмму можно интерпретировать как графическое представление эмпирической функции плотности распределения fn(x), в ней суммарная площадь всех прямоугольников составит единицу. Гистограмма помогает подобрать вид теоретической функции распределения для аппроксимации ЭД.
Полигоном называют ломаную линию, отрезки которой соединяют точки с координатами по оси абсцисс, равными серединам интервалов, а по оси ординат – соответствующим частостям. Эмпирическая функция распределения отображается ступенчатой ломаной линией: над каждым интервалом проводится отрезок горизонтальной линии на высоте, пропорциональной накопленной частости в текущем интервале. Накопленная частость равна сумме всех частостей, начиная с первого и до данного интервала включительно.
Пример 2.2. Имеются результаты регистрации значений затухания сигнала xi на частоте 1000 Гц коммутируемого канала телефонной сети. Эти значения, измеренные в дБ, в виде вариационного ряда представлены в табл. 2.3. Необходимо построить статистический ряд.
Таблица 2.3
| i | |||||||||||
| xi | 25,79 | 25,98 | 25,98 | 26,12 | 26,13 | 26,49 | 26,52 | 26,60 | 26,66 | 26,69 | 26,74 |
| i | |||||||||||
| xi | 26,85 | 26,90 | 26,91 | 26,96 | 27,02 | 27,11 | 27,19 | 27,21 | 27,28 | 27,30 | 27,38 |
| i | |||||||||||
| xi | 27,40 | 27,49 | 27,64 | 27,66 | 27,71 | 27,78 | 27,89 | 27,89 | 28,01 | 28,10 | 28,11 |
| i | |||||||||||
| xi | 28,37 | 28,38 | 28,50 | 28,63 | 28,67 | 28,90 | 28,99 | 28,99 | 29,03 | 29,12 | 29,28 |
Решение . Количество разрядов статистического ряда следует выбрать минимальным, чтобы обеспечить достаточное количество попаданий в каждый из них, возьмем y = 6. Определим размер разряда
h = (xmax – xmin)/y =(29,28 – 25,79)/6 = 0,58.
Сгруппируем наблюдения по разрядам, табл. 2.4.
Таблица 2.4
| i | ||||||
| xi | 25,79 | 26,37 | 26,95 | 27,5 3 | 28,12 | 28,70 |
| ni | ||||||
| ni =ni/n | 0,114 | 0,205 | 0,227 | 0,205 | 0,11 4 | 0,136 |
| zi =ni/h | 0,196 | 0,353 | 0,392 | 0,353 | 0,196 | 0,235 |
На основе статистического ряда построим гистограмму, рис. 2.2, и график эмпирической функции распределения, рис. 2.3.
График эмпирической функции распределения, рис. 2.3, отличается от графика, представленного на рис. 2.1 равенством шага изменения варианты и величиной шага приращения функции (при построении по вариационному ряду шаг приращения кратен
1/ n , а по статистическому ряду – зависит от частости в конкретном разряде).
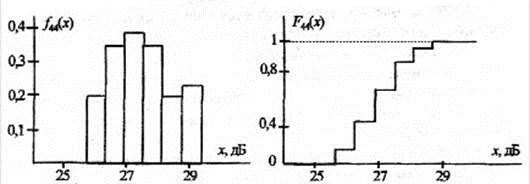
| Рис.2..2. Гистограмма распределения | Рис. 2.3. Эмпирическая функция распределения |
Рассмотренные представления ЭД являются исходными для последующей обработки и вычисления различных параметров.
Дата добавления: 2017-10-09; просмотров: 1583;
