Построение ряда распределения
Признаки, изучаемые статистикой, варьируются (отличаются друг от друга) у различных единиц совокупности в один и тот же период или момент времени. Например, величина внешнеторгового оборота варьируется по подразделениям ФТС; величина экспорта (импорта) варьируется по направлениям экспорта (по разным странам-партнерам по внешней торговле), по видам товаров и т.п.
Причиной вариации являются разные условия существования разных единиц совокупности. Например, огромное число причин влияет на масштабы внешней торговли различных стран мира.
Для управления и изучения вариации статистикой разработаны специальные методы исследования вариации, система показателей, с помощью которой вариация измеряется, характеризуются ее свойства.
Первым этапом статистического изучения вариации является построение ряда распределения (или вариационного ряда) – упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака и подсчет числа единиц с тем или иным значением признака.
Существует 3 вида ряда распределения:
1) ранжированный ряд – это перечень отдельных единиц совокупности в порядке возрастания изучаемого признака (например, таблица 11); если численность единиц совокупности достаточно велика ранжированный ряд становится громоздким, и в таких случаях ряд распределения строится с помощью группировки единиц совокупности по значениям изучаемого признака (ели признак принимает небольшое число значений, то строится дискретный ряд, а в противном случае – интервальный ряд);
2) дискретный ряд – это таблица, состоящая из двух столбцов (строк) – конкретных значений варьирующего признака Xi и числа единиц совокупности с данным значением признака fi – частот; число групп в дискретном ряду определяется числом реально существующих значений варьирующего признака;
3) интервальный ряд – это таблица, состоящая из двух столбцов (строк) – интервалов варьирующего признака Xi и числа единиц совокупности, попадающих в данный интервал (частот), или долей этого числа в общей численности совокупностей (частостей).
Построим ряд распределения внешнеторгового оборота (ВО) по таможенным постам России, для чего необходимо провести статистическое наблюдение, то есть собрать первичный статистический материал, который представляет собой величину ВО по таможенным постам.
Результаты наблюдения ВО по 35 таможенным постам региона за отчетный период представим в виде ранжированного по возрастанию величины ВО ряда распределения (таблица 11).
Таблица 11. Внешнеторговый оборот (ВО) по 35 таможенным постам, млн.долл.
| № поста | ВО | № поста | ВО | № поста | ВО |
| 24,16 | 54,12 | 65,31 | |||
| 27,06 | 54,91 | 69,24 | |||
| 29,12 | 55,74 | 71,39 | |||
| 31,17 | 55,91 | 77,12 | |||
| 37,08 | 56,07 | 79,12 | |||
| 39,11 | 56,80 | 84,34 | |||
| 41,58 | 56,93 | 86,89 | |||
| 44,84 | 57,07 | 91,74 | |||
| 46,80 | 58,39 | 96,01 | |||
| 48,37 | 59,61 | 106,84 | |||
| 51,44 | 59,95 | 111,16 | |||
| 52,56 | 62,05 | Итого | 2100,00 |
Определим средний размер ВО по формуле (10), приняв за X величину ВО, а за N – численность постов:
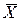 =
= 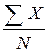 = 2100/35 = 60 (млн.долл.)
= 2100/35 = 60 (млн.долл.)
Дисперсию (о ней будет рассказано чуть позднее – на 4-м этапе анализа вариации в этой теме) определим по формуле (28):
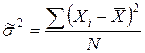 =
= 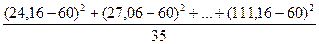 = 445,778 (млн.долл.2)
= 445,778 (млн.долл.2)
Построим интервальный ряд распределения ВО по таможенным постам, для чего необходимо выбрать оптимальное число групп (интервалов признака) и установить длину (размах) интервала. Поскольку при анализе ряда распределения сравнивают частоты в разных интервалах, необходимо, чтобы длина интервалов была постоянной[13]. Оптимальное число групп выбирается так, чтобы достаточной мере отразилось разнообразие значений признака в совокупности и в то же время закономерность распределении, его форма не искажалась случайными колебаниями частот. Если групп будет слишком мало, не проявится закономерность вариации; если групп будет чрезмерно много, случайные скачки частот исказят форму распределения.
Чаще всего число групп в ряду распределения определяют по формуле Стерждесса (19) или (20):
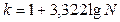 (19) или
(19) или 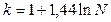 ,(20)
,(20)
где k – число групп (округляемое до ближайшего целого числа); N – численность совокупности.
Из формулы Стерджесса видно, что число групп – функция объема данных (N).
Зная число групп, рассчитывают длину (размах) интервала[14] по формуле (21):
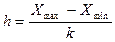 ,(21)
,(21)
где Xмax и Xmin — максимальное и минимальное значения в совокупности.
В нашем примере про ВО по формуле Стерждесса (19) определим число групп:
k = 1 + 3,322lg35 = 1+ 3,322*1,544 = 6,129 ≈ 6.
Рассчитаем длину (размах) интервала по формуле (21):
h = (111,16 – 24,16)/6 = 87/6 = 14,5 (млн.долл.).
Теперь построим интервальный ряд с 6 группами с интервалом 14,5 млн.долл. (см. первые 3 столбца табл. 12).
Таблица 12. Интервальный ряд распределения ВО по таможенным постам, млн.долл.
| i | Группы постов по величине ВО Xi | Число постов fi | Середина интервала Хi’ | Хi’fi | Накопл. частота fi’ | | Хi’ - 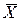 | fi | fi
| (Хi’ - 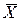 )2 fi )2 fi
| (Хi’ - 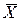 )3 fi )3 fi
| (Хi’ - 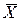 )4 fi )4 fi
|
| 24,16 – 38,66 | 31,41 | 157,05 | 147,071 | 4326,001 | -127246,23 | 3742856,97 | |||
| 38,66 – 53,16 | 45,91 | 321,37 | 104,400 | 1557,051 | -23222,31 | 346344,16 | |||
| 53,16 – 67,66 | 60,41 | 785,33 | 5,386 | 2,231 | -0,92 | 0,38 | |||
| 67,66 – 82,16 | 74,91 | 299,64 | 56,343 | 793,629 | 11178,84 | 157461,90 | |||
| 82,16 – 96,66 | 89,41 | 357,64 | 114,343 | 3268,572 | 93434,47 | 2670891,13 | |||
| 96,66 – 111,16 | 103,91 | 207,82 | 86,171 | 3712,758 | 159966,81 | 6892284,32 | |||
| Итого | 2128,85 | 513,714 | 13660,243 | 114110,66 | 13809838,86 |
Существенную помощь в анализе ряда распределения и его свойств оказывает графическое изображение. Интервальный ряд изображается столбиковой диаграммой, в которой основания столбиков, расположенные по оси абсцисс, – это интервалы значений варьирующего признака, а высоты столбиков – частоты, соответствующие масштабу по оси ординат. Графическое изображение распределения таможенных постов в выборке по величине ВО приведено на рис. 4. Диаграмма такого типа называется гистограммой[15].
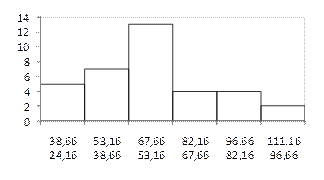
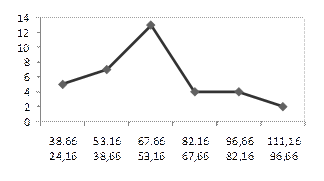
Рис. 4. Гистограмма распределения Рис. 5. Полигон распределения
Данные табл. 12 и рис. 4 показывают характерную для многих признаков форму распределения: чаще встречаются значения средних интервалов признака, реже – крайние (малые и большие) значения признака. Форма этого распределения близка к нормальному закону распределения, которое образуется, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего значения.
Если имеется дискретный ряд распределения или используются середины интервалов (как в нашем примере про ВО – в таблице 12 в 4-м столбце рассчитаны середины интервалов как полусумма значений начала и конца интервала), то графическое изображение такого ряда называется полигоном (см. рис. 5)[16], которое получается соединением прямыми точек с координатами Xi и fi.
Дата добавления: 2017-09-19; просмотров: 611;
