Относительные величины
Относительная величина – это результат деления (сравнения) двух абсолютных величин. В числителе дроби стоит величина, которую сравнивают, а в знаменателе – величина, с которой сравнивают (база сравнения). Например, если сопоставить величины экспорта США и России, которые в 2005 году составили 904,383 и 243,569 млрд. долл. соответственно, то относительная величина покажет, что величина экспорта США в 3,71 раза (904,383/243,569) больше экспорта России, при этом базой сравнения является величина экспорта России. Полученная относительная величина выражена в виде коэффициента, который показывает, во сколько раз сравниваемая абсолютная величина больше базисной. В данном примере база сравнения принята за единицу. В случае если основание принимается за 100, относительная величина выражается в процентах (%), если за 1000 – в промилле (‰). Выбор той или иной формы относительной величины зависит от ее абсолютного значения:
– если сравниваемая величина больше базы сравнения в 2 раза и более, то выбирают форму коэффициента (как в вышеприведенном примере);
– если относительная величина близка к единице, то, как правило, ее выражают в процентах (например, сравнив величины экспорта России в 2006 и 2005 годах, которые составили 304,5 и 243,6 млрд. долл. соответственно, можно сказать, что экспорт в 2006 году составляет 125% от 2005 года [304,5/243,6*100%]);
– если относительная величина значительно меньше единицы (близка к нулю), ее выражают в промилле (например, в 2004 году Россия экспортировала в страны-СНГ всего 4142 тыс. т нефтепродуктов, в том числе в Грузию 10,7 тыс. т, что составляет 0,0026 [10,7/4142], или 2,6‰ от всего экспорта нефтепродуктов в страны СНГ).
Различают относительные величины динамики, структуры, координации, сравнения и интенсивности, для краткости именуемые в дальнейшем индексами.
Индекс динамики[9] характеризует изменение какого-либо явления во времени. Он представляет собой отношение значений одной и той же абсолютной величины в разные периоды времени. Данный индекс определяется по формуле (2):
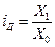 , (2)
, (2)
где цифры означают: 1 – отчетный или анализируемый период, 0 – прошлый или базисный период.
Критериальным значением индекса динамики служит единица (или 100%), то есть если 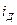 >1, то имеет место рост (увеличение) явления во времени; если
>1, то имеет место рост (увеличение) явления во времени; если 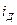 =1 – стабильность; если
=1 – стабильность; если 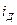 <1 – наблюдается спад (уменьшение) явления. Еще одно название индекса динамики – индекс изменения, вычитая из которого единицу (100%), получают темп изменения (динамики)[10] с критериальным значением 0, который определяется по формуле (3):
<1 – наблюдается спад (уменьшение) явления. Еще одно название индекса динамики – индекс изменения, вычитая из которого единицу (100%), получают темп изменения (динамики)[10] с критериальным значением 0, который определяется по формуле (3):
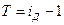 . (3)
. (3)
Если T>0, то имеет место рост явления; Т=0 – стабильность, Т<0 – спад.
В рассмотренном выше примере про экспорт России в 2006 и 2005 году был рассчитан именно индекс динамики по формуле (2): iД = 304,5/243,6*100% = 125%, что больше критериального значения 100%, что свидетельствует об увеличении экспорта. Используя формулу (3) получим темп изменения: Т = 125% – 100% = 25%, который показывает, что экспорт увеличился на 25%.
Разновидностями индекса динамики являются индексы планового задания и выполнения плана, рассчитываемые для планирования различных величин и контроля их выполнения.
Индекс планового задания – это отношение планового значения признака к базисному. Он определяется по формуле (4):
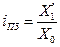 , (4)
, (4)
где X’1 – планируемое значение; X0 – базисное значение признака.
Например, таможенное управление перечислило в федеральный бюджет в 2006 году 160 млрд.руб., а на следующий год запланировали перечислить 200 млрд.руб., значит по формуле (4): iпз = 200/160 = 1,25, то есть плановое задание для таможенного управления на 2007 год составляет 125% от предыдущего года.
Для определения процента выполнения плана необходимо рассчитать индекс выполнения плана, то есть отношение наблюдаемого значения признака к плановому (оптимальному, максимально возможному) значению по формуле (5):
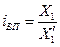 . (5)
. (5)
Например, на январь-ноябрь 2006 года таможенные органы запланировали перечислить в федеральный бюджет 1,955 трлн. руб., но фактически перечислили 2,59 трлн. руб., значит по формуле (5): iВП = 2,59/1,955 = 1,325, или 132,5%, то есть плановое задание выполнили на 132,5%.
Индекс структуры (доля) – это отношение какой-либо части объекта (совокупности) ко всему объекту. Он определяется по формуле (6):
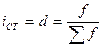 (6)
(6)
В рассмотренном выше примере про экспорт нефтепродуктов в страны СНГ, была рассчитана доля этого экспорта в Грузию по формуле (6): d=10,7/4142 = 0,0026, или 2,6‰.
Индекс координации – это отношение какой-либо части объекта к другой его части, принятой за основу (базу сравнения). Он определяется по формуле (7):
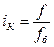 . (7)
. (7)
Например, импорт России в 2006 году составил 163,9 млрд.долл., тогда, сравнив его с экспортом (база сравнения), рассчитаем индекс координации по формуле (7): iК = 163,9/304,5 = 0,538, который показывает соотношение между двумя составными частями внешнеторгового оборота, то есть величина импорта России в 2006 году составляет 53,8% от величины экспорта. Меняя базу сравнения на импорт, по той же формуле получим: iК = 304,5/163,9 = 1,858, то есть экспорт России в 2006 году в 1,858 раза больше импорта, или экспорт составляет 185,8% от импорта.
Индекс сравнения – это сравнение (соотношение) разных объектов по одинаковым признакам. Он определяется по формуле (8):
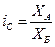 , (8)
, (8)
где А, Б – сравниваемые объекты.
В рассмотренном выше примере, в котором сопоставлялись величины экспорта США и России, был рассчитан именно индекс сравнения по формуле (8): iс = 904,383/243,569 = 3,71. Меняя базу сравнения (то есть экспорт России – объект А, а экспорт США – объект Б), по той же формуле получим: iс = 243,569/904,383 = 0,27, то есть экспорт России составляет 27% от экспорта США.
Индекс интенсивности – это соотношение разных признаков одного объекта между собой. Он определяется по формуле (9):
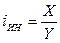 . (9)
. (9)
где X – один признак объекта; Y – другой признак этого же объекта
Например, показатели выработки продукции в единицу рабочего времени, затрат на единицу продукции, цены единицы продукции и т.д.
Средние величины
Как уже неоднократно было сказано ранее, статистика изучает массовые явления и процессы. Каждое из таких явлений обладает как общими для всей совокупности, так и особенными, индивидуальными свойствами. Различие между индивидуальными явлениями называют вариацией, о ней подробно будет рассказано в теме 3. Здесь же рассмотрим другое свойство массовых явлений – присущую им близость характеристик отдельных явлений. В этом свойстве заключается причина широчайшего применения средних величин. Главное значение средних величин состоит в их обобщающей функции, то есть замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.
Виды средних величин различаются прежде всего тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным.
Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности. Исходя из определения, формула средней арифметической величины имеет вид (10):
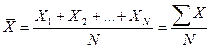 . (10)
. (10)
По формуле (10) вычисляются средние величины первичных признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку, как, например, табл. 3.
Таблица 3. Распределение студентов группы дневного отделения по возрасту
| Возраст студентов, X | |||||
| Число студентов, f |
Средний возраст должен представлять собой результат равномерного распределения общего (суммарного) возраста всех студентов. Общий (суммарный) возраст всех студентов, согласно исходной информации табл. 3, можно получить как сумму произведений значений признакав каждой группе Xi, на число студентов с таким возрастом fi (частоты). Получим формулу (11):
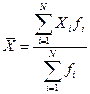 , (11)
, (11)
где i – число групп.
Такую форму средней арифметической величины называют взвешенной арифметической средней[11] в отличие от простой средней, рассчитанной по формуле (10). В качестве весов здесь выступают количество единиц совокупности в разных группах. Название «вес» выражает тот факт, что разные значения признака имеют неодинаковую «важность» при расчете средней величины. «Важнее», весомее возраст студентов 18, 19, 20 лет, а такие значения возраста как 17, 20 или 21 при расчете средней не играют большой роли – их «вес» мал.
По формуле (11) по данным табл. 3 имеем:
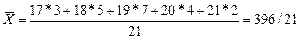 = 18,857 (лет).
= 18,857 (лет).
Как видим, средняя арифметическая величина может быть дробным числом, если даже индивидуальные значения признака могут принимать только целые значения. Ничего необычного для метода средних в этом не заключено, так как из сущности средней не следует, что она обязана быть реальным значением признака, которое могло бы встретиться у какой-либо единицы совокупности.
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, то есть исходят из предположения о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств признака и совокупности. При отсутствии возможности экспертной оценки значения признака в открытых интервалах, для нахождения недостающей границы открытого интервала применяют размах (разность между значениями конца и начала интервала) соседнего интервала (принцип «соседа»).
Например, по данным табл. 4 можно минимальную и максимальную величину веса студентов определить затруднительно, поэтому воспользуемся принципом «соседа» – применим размах соседнего интервала, который у второго и предпоследнего составляет 10 кг, значит первый интервал будет от 50 до 60 кг, а последний – от 80 до 90 кг. Середины интервалов определяем как полусумму нижней и верхней границы интервалов.
Таблица 4. Распределение студентов по весу
| Группы студентов по весу, кг | Количество студентов, чел. | Середина интервала Xi’ | Xi’fi |
| До 60 | |||
| 60 – 70 | |||
| 70 – 80 | |||
| Более 80 | |||
| Итого | 66,429 |
Средний вес студентов, рассчитанный по формуле (11) с заменой точных значений признака в группах серединами интервалов, составил:
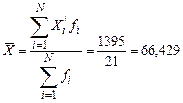 кг,
кг,
что и записано в итоговую строку в 3-м столбце табл. 4. Следует обратить внимание, что итог объемного показателя – это сумма, а итог по столбцам относительных показателей или средних групповых величин – средняя.
Средняя арифметическая величина обладает свойствами, знание которых полезно как при ее использовании, так и при ее расчете.
1. Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю. Доказательство[12]:
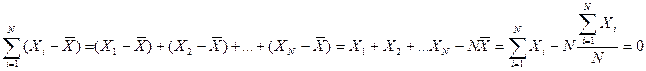
2. Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшится во столько же раз. Доказательство:
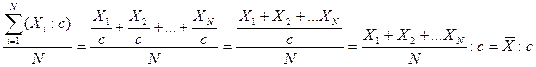
Вследствие этого свойства индивидуальные значения признака можно сократить в c раз, произвести расчет средней и результат умножить на c.
3. Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то средняя величина возрастет или уменьшится на это же число. Доказательство:
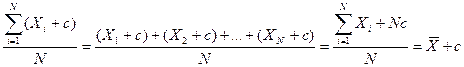
Это свойство полезно использовать при расчете средней величины из многозначных и слабоварьирующих значений признака аналогично предыдущему свойству.
4. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится. Доказательство:
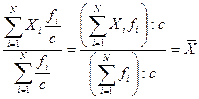
Используя это свойство, при расчетах следует сокращать веса на их общий сомножитель либо выражать многозначные числа весов в более крупных единицах измерениях.
5. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа. Доказательство: составим сумму квадратов отклонений от переменной a: 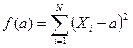 , чтобы найти экстремум этой функции, найдем ее производную по a и приравняем ее нулю, т.е.
, чтобы найти экстремум этой функции, найдем ее производную по a и приравняем ее нулю, т.е. 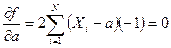 , отсюда получаем
, отсюда получаем 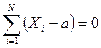 ;
; 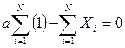 ;
; 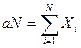 ;
; 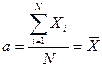 . Таким образом, экстремум суммы квадратов отклонений достигает максимума при a=
. Таким образом, экстремум суммы квадратов отклонений достигает максимума при a= 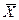 . Так как логически ясно, что максимума функция иметь не может, этот экстремум является минимумом.
. Так как логически ясно, что максимума функция иметь не может, этот экстремум является минимумом.
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменную сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной. Ее формула следующая:
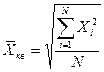 . (12)
. (12)
Главной сферой применения квадратической средней в силу пятого свойства средней арифметической величины является измерение вариации признака в совокупности.
Аналогично, если по условиям задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, мы приходим к средней кубической величине, имеющей вид:
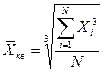 . (13)
. (13)
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину, имеющую следующий вид:
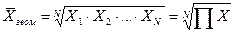 . (14)
. (14)
Основное применение средняя геометрическая находит при определении средних относительных изменений, о чем сказано в теме 6. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения признака, который качественно был бы равноудален как от максимального, так и от минимального значения признака.
Когда статистическая информация не содержит частот f по отдельным вариантам Xi совокупности, а представлена как их произведение Xf, тогда применяется формула средней гармонической взвешенной, для получения которой обозначим Xf=w, откуда f=w/X, и, подставив эти обозначения в формулу (11), получим формулу (15):
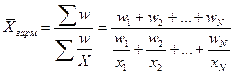 . (15)
. (15)
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны действительные веса f, а известно w=Xf. В тех случаях, когда вес каждого варианта w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой (16):
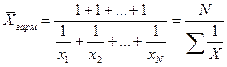 . (16)
. (16)
Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних, имеющему следующий вид:
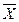 =
= 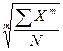 . (17)
. (17)
При m = 1 получаем среднюю арифметическую; при m = 2 – среднюю квадратическую;
при m = 3 – среднюю кубическую; при m = 0 – среднюю геометрическую; при m = –1 – среднюю гармоническую. Чем выше показатель степени m, тем больше значение средней величины (если индивидуальные значения признака варьируют). В итоге, можно построить следующее соотношение, которое называется правилом мажорантности средних:
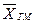 ≤
≤ 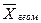 ≤
≤ 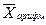 ≤
≤ 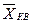 ≤
≤ 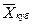 . (18)
. (18)
Дата добавления: 2017-09-19; просмотров: 1155;
