Зв’язок між характеристичною функцією цілочислових дискретних випадкових величин та генератрисою

Нехай 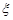– дискретна випадкова величини, яка набуває тільки цілі невід’ємні значення та має генератрису 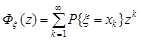. Якщо зробити заміну змінної 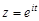, то генератриса набуває вигляду 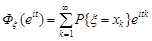. Порівнюючи цю формулу з формулою (22.2), бачимо, що

,

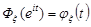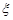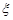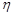тобто співпадає з характеристичною функцією випадкової величини . Отже, генератриса має властивості аналогічні властивостям характеристичної функції. Наприклад, генератриса суми двох незалежних дискретних випадкових величин та дорівнює добутку їх генератрис

.

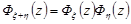Ця формула узагальнюється на суму незалежних у сукупності дискретних випадкових величин:

.

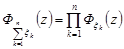Нагадаємо, що цією властивістю користуються при знаходженні композицій законів розподілу.

Приклад 22.6. Випадкові величини 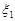та 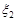незалежні та мають геометричні розподіли з однаковим параметром 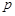. Скласти закон розподілу їх суми .

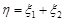Розв’язання. Оскільки випадкові величини 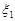та 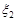розподілені однаково за геометричним законом, то їх генератриси дорівнюють

.

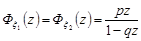Відповідно генератриса їх суми має вигляд

.

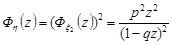Для складання ряду розподілу випадкової величини 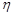треба останній вираз розкласти в ряд Маклорена:

.

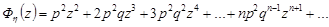Отже, випадкова величина 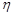набуває значення 2, 3, 4, ..., 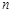,... з імовірностями, що дорівнюють коефіцієнтам при відповідних степенях 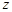в отриманому розкладанні.