Характеристичні функції випадкових величин та їх властивості

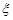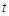Означення 22.1. Характеристичною функцією випадкової величини називається математичне сподівання комплексно значної випадкової величини , де – будь-яке дійсне число, 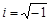, тобто

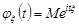. (22.1)

Для дискретних випадкових величин 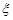формула (22.1) розписується так:

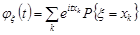, (22.2)

а для неперервної випадкової величини 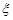із щільністю розподілу 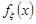характеристична функція

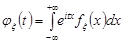. (22.3)

При проведенні деяких досліджень розумно домовитись позначати праві частини у формулах (22.2) та (22.3) однаково, використовуючи функцію розподілу 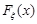випадкової величини 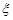, а саме

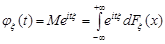. (22.4)

Неважко побачити, що характеристична функція 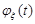є перетворення Фур’є функції розподілу .

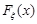Із курсу математичного аналізу відомі формули оберненого перетворення, тобто щільність розподілу неперервної випадкової величини 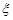дорівнює

,

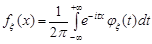а для дискретної випадкової величини можна записати

.

Таким чином, визначення випадкової величини 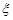за допомогою характеристичної функції еквівалентне визначенню через щільність розподілу у неперервному випадку або ряд розподілу у дискретному.

Наведемо основні властивості характеристичних функцій.

1. Характеристична функція будь-якої випадкової величини 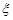в нулі набуває значення 1, тобто .

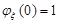2. Модуль характеристичної функції не перевищує одиниці

.

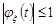Доведення. Проведемо доведення для характеристичних функцій неперервних випадкових величин.

.

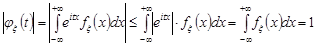3. Характеристична функція 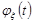є рівномірно неперервною функцією на всій осі.

Доведення. Для доведення зробимо оцінку

.

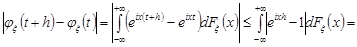
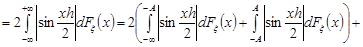
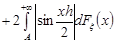Права частина цієї нерівності не залежить від 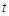. Перший та третій інтеграли можна зробити як завгодно малими за рахунок вибору числа 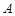, а другий інтеграл можна зробити як завгодно малими за рахунок вибору величини .

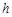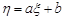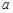4. Якщо випадкова величина , де та 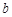– сталі величини, то

.

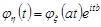Доведення. За означенням характеристичної функції (22.1) та властивостями математичного сподівання маємо

.

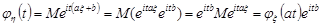5. Характеристична функція суми двох незалежних випадкових величин 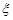та 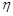дорівнює добутку їх характеристичних функцій

.

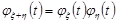Доведення. Якщо випадкові величини 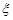та 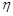незалежні, то випадкові величини і 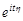також будуть незалежними. Отже, математичне сподівання добутку цих величин дорівнює добутку математичних сподівань

.

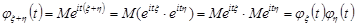Цю властивість неважко узагальнити на суму незалежних у сукупності випадкових величин

.

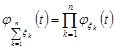6. Між початковими моментами випадкової величини 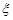та її характеристичною функцією існує такий зв’язок

.

Доведення. Оскільки інтеграл 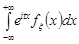збігається рівномірно на всій числовій осі, то можлива операція диференціювання під знаком інтегралу, тобто

.

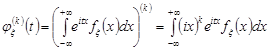Звідси маємо

.

7. За характеристичною функцією можна знаходити числові характеристики випадкової величини.

Доведення. Дійсно, з властивості 6 маємо, що математичне сподівання випадкової величини 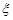дорівнює

.

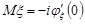Відповідно дисперсію випадкової величини 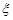знайдемо за формулою

.

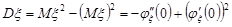8. .

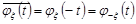Доведення.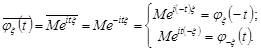

9. Характеристична функція випадкової величини 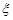є дійсно значною лише тоді і тільки тоді, коли розподіл випадкової величини є симетричним відносно нуля.

Доведення. Доведення проведемо для неперервної випадкової величини. Враховуючи, що 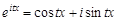, характеристичну функцію можна записати так

.

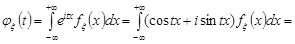
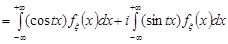Якщо закон розподілу випадкової величини 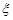є симетричним відносно нуля, то щільність розподілу 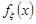– парна функція, тод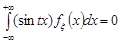і і

,

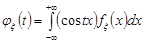тобто є дійсно значною функцією. Якщо ж за припущенням характеристична функція 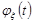є дійсно значною, то за 8 властивістю

,

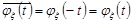тобто характеристична функція 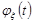є парною, отже, закон розподілу випадкової величини 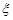є симетричним відносно нуля.

Приклад 22.1.Знайти щільність розподілу ймовірностей 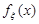випадкової величини 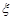, характеристична функція якої має вигляд:

.

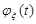
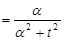Розв’язання. Закон розподілу випадкової величини 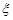знайдемо за формулою (4.10):

= .

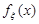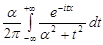Для обчислення інтеграла застосуємо теорему про лишки.

При х < 0

.

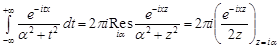
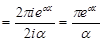Аналогічно при х > 0

.

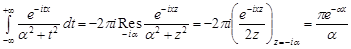Остаточно маємо: 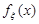= 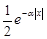. Розподіл, який має таку щільність, називається розподілом Лапласа.

22.2. Характеристичні функції деяких розподілів

Наведемо приклади характеристичних функцій деяких законів розподілу.

1. Біномний розподіл. За формулою (22.2)

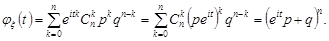
2. Розподіл Пуассона.

.

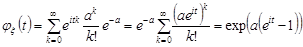3. Геометричний розподіл.

.

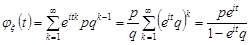4. Рівномірний розподіл на 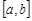. За формулою (22.3)

.

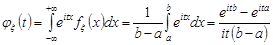Зокрема, якщо проміжок симетричний відносно 0, наприклад, 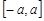, то характеристична функція набуває вигляду

.

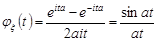5. Закон Гаусса .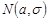

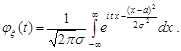
Розглянемо показник підінтегральної функції і виділимо в ньому повний квадрат

.

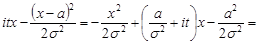
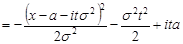Записуємо характеристичну функцію так

.

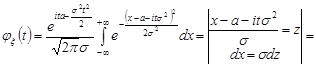
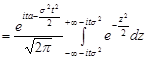Інтеграл, що входить до правої частини є інтеграл Пуассона, який дорівнює 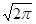. Отже,

.

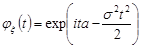6. Показниковий розподіл.

.

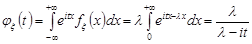Приклад 22.2. Обчислити другий початковий момент 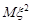випадкової величини 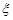розподіленої за біномним законом.

Розв’язання. Для обчислення другого початкового моменту випадкової величини 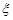, яка розподілена за біномним законом, використаємо характеристичну функцію цього закону та властивість 6 характеристичних функцій, тоді .

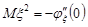Знайдемо другу похідну від характеристичної функції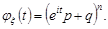

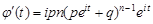
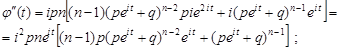
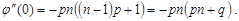
Отже, .

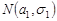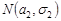Приклад 22.3.Скласти композицію двох нормальних законів розподілу та відповідно.

Розв’язання. Нехай випадкова величина 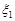має нормальний закон розподілу з параметрами 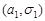, а 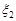– нормальний закон розподілу з параметрами 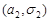. Треба знайти закон розподілу суми незалежних випадкових величин 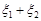. За властивістю 5 характеристична функція суми незалежних випадкових величин дорівнює

.

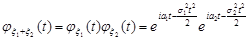
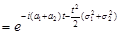Отже, з цієї формули випливає , що це – характеристична функція нормального закону з параметрами 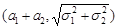. Результат задачі показує, що закон Гаусса стійкий.

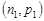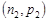Приклад 22.4. Скласти композицію двох законів Бернуллі з параметрами та відповідно.

Розв’язання. Аналогічно характеристична функція суми двох незалежних випадкових величин, розподілених за біномним законом дорівнює

.

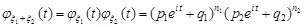Очевидно, розподіл суми буде біномним тільки тоді, коли 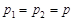. В цьому випадку 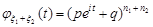, тобто параметри розподілу суми будуть .