Характеристичні функції випадкових векторів та їх властивості
Означення 22.2. Характеристичною функцією випадкового вектора 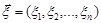 називається функція вигляду
називається функція вигляду
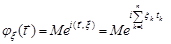 , (22.5)
, (22.5)
де 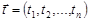 .
.
Якщо 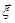 неперервний вектор із щільністю розподілу
неперервний вектор із щільністю розподілу 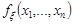 , то формула (22.5) набуває вигляд
, то формула (22.5) набуває вигляд
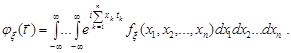
У випадку дискретного випадкового вектора 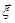 формула (22.5) буде такою
формула (22.5) буде такою
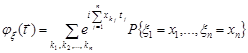 .
.
Властивості характеристичних функцій випадкових векторів аналогічні властивостям характеристичних функцій випадкового вектора. Назвемо їх.
1. Характеристична функція випадкового вектора повністю визначає випадковий вектор.
2. 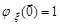 ,
, 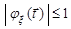 .
.
3. Характеристична функція 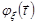 рівномірно неперервна в просторі
рівномірно неперервна в просторі 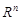 .
.
4. Якщо компоненти випадкового вектора 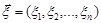 незалежні у сукупності, то
незалежні у сукупності, то
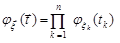 ,
,
де 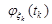 – характеристична функція компоненти
– характеристична функція компоненти 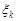 ,
, 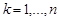 .
.
5.Якщо випадковий вектор 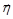 є афінне перетворення випадкового вектора
є афінне перетворення випадкового вектора 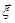 , тобто
, тобто 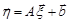 , то
, то
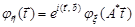 ,
,
де 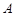 та
та 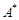 спряжені матриці.
спряжені матриці.
6. Моменти розподілу можна обчислювати через характеристичну функцію за формулою
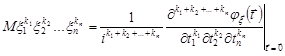 .
.
22.4. Характеристична функція гауссівського вектору
Як приклад характеристичної функції випадкових векторів, розглянемо характеристичну функцію гауссівського випадкового вектору.
Для отримання характеристичної функції 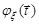 нормально розподіленого випадкового вектора
нормально розподіленого випадкового вектора 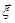 виберемо в
виберемо в 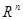 ортобазис із власних векторів
ортобазис із власних векторів 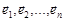 кореляційної матриці
кореляційної матриці 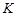 . Тоді за формулою (19.2) щільність розподілу вектора
. Тоді за формулою (19.2) щільність розподілу вектора 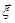 має вигляд
має вигляд
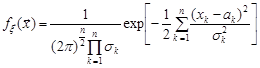 .
.
Враховуючи означення характеристичної функції випадкового вектора та властивість 4, маємо
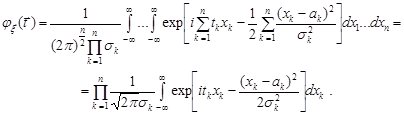
Але вираз, що стоїть під знаком добутку є не що інше, як характеристична функція гауссівської випадкової величини, параметри якої дорівнюють 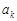 та
та 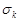 . Таким чином,
. Таким чином,
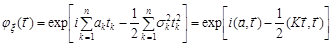 .
.
Приклад 22.5. Знайти числові характеристики нормально розподіленого випадкового вектора 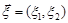 , характеристична функція якого має вигляд
, характеристична функція якого має вигляд
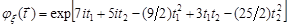 .
.
Розв’язання. Скористаємось властивістю 6 характеристичної функції та знайдемо відповідні моменти випадкового вектора
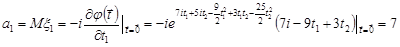 .
.
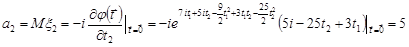 .
.
Отже, центр розсіювання заданого випадкового вектора 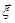 є точка з координатами
є точка з координатами 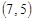 .
.
Обчислимо другі моменти випадкового вектора.
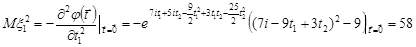 .
.
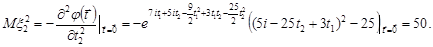
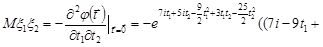
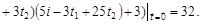
Отже, дисперсії компонент випадкового вектора дорівнюють 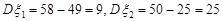 , а кореляційний момент
, а кореляційний момент 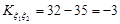 . Таким чином, кореляційна матриця має вигляд
. Таким чином, кореляційна матриця має вигляд
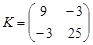 .
.
Дата добавления: 2017-02-20; просмотров: 1150;
