Види збіжностей послідовності випадкових величин

Приклади послідовностей випадкових величин

Нехай на деякому імовірнісному просторі 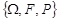задана послідовність випадкових величин 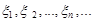, тобто вказане правило, за яким визначається член цієї послідовності в залежності від його номера n.

Розглянемо деякі приклади задання послідовностей випадкових величин.

Приклад 24.1. Задамо випадкову величину 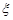. Із цією випадковою величиною можна пов’язати різні послідовності випадкових величин, наприклад,

1)

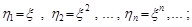
2)

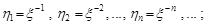
3)

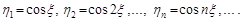
Приклад 24.2. Задана послідовність неперервних випадкових величин 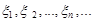, щільність розподілу 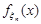кожної з яких має вигляд:

1)

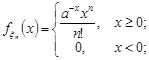
2)

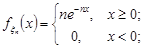
3) .

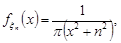
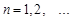Приклад 24.3. Задана послідовність дискретних випадкових величин 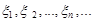, ряди розподілів яких мають вигляд:

1)

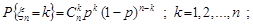
2) 3)

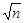
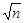
xn	–				xn	–3n		3n
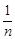
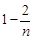
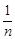
р					р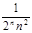

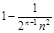
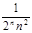
Види збіжностей послідовності випадкових величин

Як і в детермінованому випадку слід ввести поняття збіжності та границі послідовності випадкових величин. Зрозуміло, що тут виникають ті ж самі проблеми, що й при дослідженні детермінованих (невипадкових) функціональних послідовностей, тобто матимемо справу із різними поняттями збіжності послідовності випадкових величин.

Означення 24.1. Послідовність випадкових величин 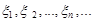називається збіжною за ймовірністю до випадкової величини 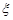, якщо при будь-якому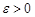

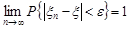
або, теж саме,

.

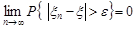Аналогом цієї збіжності в теорії функцій є збіжність за мірою.

Скорочено збіжність за ймовірністю позначають так:

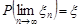або .

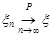Зокрема, послідовність випадкових величин може збігатися за ймовірністю не тільки до випадкової величини, а й до деякої сталої.

Означення 24.2. Послідовність випадкових величин 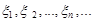збігається за розподілом до випадкової величини 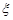, якщо послідовність функцій розподілу 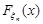членів послідовності 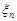збігається до функції розподілу 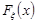випадкової величини 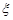в кожній точці x, для якої 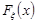неперервна.

Зауважимо, що послідовність функцій розподілу 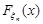, збігається до функції 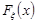в кожній точці х тоді та тільки тоді, коли послідовність характеристичних функцій елементів послідовності 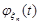збігається до характеристичної функції 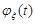випадкової величини 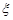в кожній точці .

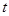Збіжність за розподілом використовують при апроксимації одного розподілу іншим. Прикладом може бути збіжність біноміального розподілу до пуассонівського.

Будемо вважати, що всі члени випадкової послідовності 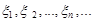визначені на одному імовірнісному просторі .

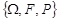Означення 24.3. Послідовність випадкових величин 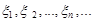називається збіжною за ймовірністю 1 до випадкової величини 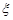, якщо 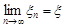майже для всіх точок 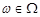, за виключенням можливо множини тих точок, імовірність яких дорівнює 0.

Отже, збіжність за ймовірністю 1 означає, що 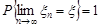. Аналогом цієї збіжності в теорії функцій є збіжність майже всюди.

Означення 24.4. Послідовність випадкових величин 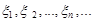називається збіжною в середньому квадратичному до випадкової величини 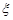, якщо

.

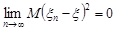Формально ця збіжність позначається так

,

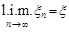де 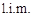– перші літери латинських слів “limes in media”.

Означення 24.5. Послідовність випадкових величин 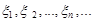називається збіжною в середньому до випадкової величини 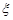, якщо

.

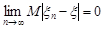Приклад 24.2. Нехай випадкова величина 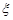розподілена за законом Пуассона з параметром λ, тобто

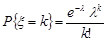; k = 0, 1, 2, ... .

Розглянемо випадкову послідовність 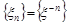. Довести, що ця послідовність не збігається за ймовірністю до 0.

Доведення. Візьмемо величину 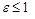, тоді 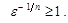Зробимо оцінку

.

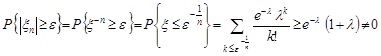Приклад 24.3. Довести, що послідовність випадкових величин { 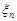}, щільність розподілу кожної із яких має вигляд

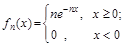
збігається за імовірністю до 0.

Доведення. Візьмемо будь-яку величину 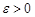. Зробимо оцінку

.

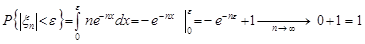Можна довести, що збіжність послідовності випадкових величин 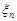до величини 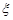за розподілом та за ймовірністю еквівалентні. Із збіжності в середньому випливає збіжність за ймовірністю. Із збіжності у середньому квадратичному випливає збіжність і за імовірністю, і в середньому.

Нерівність Маркова

Нерівність Маркова. (лема Чебишева). Якщо випадкова величина 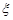набуває тільки невід’ємних значень і має математичне сподівання, тоді для будь-якої величини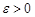

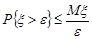. (24.1)

Доведення. Доведення проведемо для неперервної випадкової величини 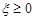, яка має щільність розподілу 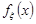. Візьмемо будь-яку величину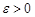

.

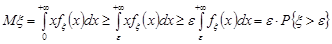Із цієї оцінки випливає нерівність (24.1). Для дискретних випадкових величин доведення проведіть аналогічно.

Приклад 24.4. Середня кількість викликів, що поступають на комутатор протягом години, дорівнює 300. Оцінити ймовірність того, що протягом наступної години кількість викликів на комутатор: 1) перевищить 400; 2) буде не більше 500.

Розв’язання. Кількість викликів, що поступають на комутатор протягом години, є випадкова величина 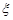. За умовою задачі 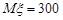. За формулою (24.1)

,

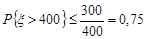тобто, ймовірність того, що кількість викликів перевищить протягом наступної години 400, буде не більше 0,75.

Аналогічно за формулою (24.1)

,

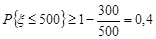тобто ймовірність того, що кількість викликів буде не більше 500, буде не менше ніж 0,4.

Приклад 24.5. Сума всіх внесків у відділення банку складає 2 млн. грн., а імовірність того, що випадково взятий вклад не перевищить 10 тис. грн. дорівнює 0,6. Що можна сказати про кількість вкладників?

Розв’язання. Нехай випадкова величина 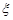задає розмір випадково взятого вкладу, а 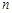дорівнює кількості вкладників. Тоді за умовою задачі 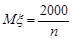(тис. грн.). За нерівністю Маркова

.

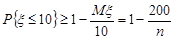Врахуємо, що 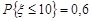. Отже, 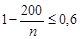. Звідси маємо, що .

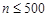Застосовуючи нерівність Маркова можна довести, що із збіжності в середньому випливає збіжність за ймовірністю. Проведіть доведення самостійно.