Нерівність Чебишева
Доведення багатьох подальших фактів базується на нерівності Чебишева.
Нерівність Чебишева. Для будь-якої випадкової величини 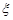 , що має математичне сподівання та обмежену дисперсію, при будь-якому
, що має математичне сподівання та обмежену дисперсію, при будь-якому 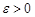 справедлива нерівність
справедлива нерівність
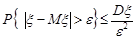 . (24.2)
. (24.2)
Доведення. Нерівність очевидна, якщо 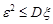 . Проведемо доведення для неперервної випадкової величини
. Проведемо доведення для неперервної випадкової величини 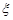 , яка має щільність розподілу
, яка має щільність розподілу 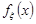 . Візьмемо
. Візьмемо 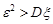 .
.
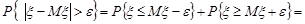
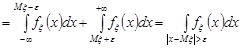 .
.
Запишемо дисперсію випадкової величини 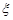
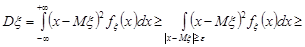
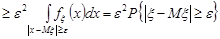 .
.
Звідси маємо нерівність (24.2). Доведення для дискретних випадкових величин проведіть аналогічно.
Враховуючи, що події 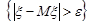 та
та 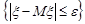 протилежні, маємо наслідок із формули (24.2):
протилежні, маємо наслідок із формули (24.2):
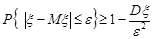 . (24.3)
. (24.3)
Нерівність Чебишева справедлива для будь-яких випадкових величин. У вигляді (24.2) вона встановлює верхню границю, а у вигляді (24.3) – нижню границю ймовірності відповідної події.
Запишемо нерівність Чебишева для деяких випадкових величин.
1. Нехай випадкова величина 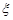 розподілена за біномним законом із параметрами
розподілена за біномним законом із параметрами 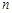 та
та 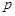 , тоді
, тоді  і
і 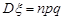 . Формула (24.3) набуває вигляду
. Формула (24.3) набуває вигляду
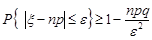 .
.
2. Для частості 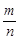 події в
події в 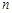 незалежних випробуваннях маємо відповідно таку оцінку
незалежних випробуваннях маємо відповідно таку оцінку
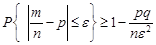 .
.
Приклад 24.6. Випадкова величина 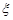 має щільність розподілу
має щільність розподілу 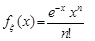 , при
, при 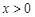 . Довести нерівність
. Довести нерівність
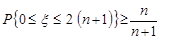 .
.
Доведення. Обчислимо числові характеристики 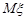 та
та 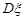 .
.
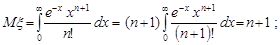
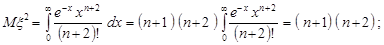
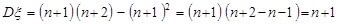 .
.
За нерівністю Чебишева:
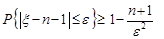 .
.
Покладемо 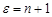 , тоді
, тоді
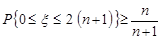 .
.
Приклад 24.7. Оцінити ймовірність того, що відхилення будь-якої випадкової величини від її математичного сподівання за абсолютною величиною буде не більше трьох стандартних відхилень (правило “3 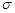 ”).
”).
Розв’язання. За формулою (24.3) маємо
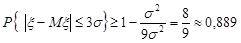 .
.
Нагадаємо, що для нормально розподіленої випадкової величини правило “3 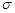 ” виконується з імовірністю 0,9973. Покажіть, що для рівномірного закону це правило виконується з імовірністю 1, а для показникового – 0,9827. Отже, правило “3
” виконується з імовірністю 0,9973. Покажіть, що для рівномірного закону це правило виконується з імовірністю 1, а для показникового – 0,9827. Отже, правило “3 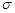 ” (з достатньо великою ймовірністю його виконання) може бути використано для більшості випадкових величин.
” (з достатньо великою ймовірністю його виконання) може бути використано для більшості випадкових величин.
Приклад 24.8. Довести, що послідовність випадкових величин { 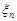 }, ряд розподілу кожної з яких має вигляд
}, ряд розподілу кожної з яких має вигляд
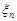
| 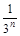
| 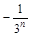
|
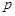
| 0,5 | 0,5 |
збігається за ймовірністю до 0.
Доведення. Обчислимо числові характеристики 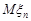 та
та 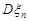 . За рядом розподілу маємо
. За рядом розподілу маємо
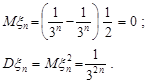
За нерівністю Чебишева
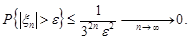
Дата добавления: 2017-02-20; просмотров: 2472;
