Язык регулярных выражений
Язык регулярных выражений предложен американским ученым С. К. Клини в 1956 г. и усовершенствован советским ученым В. М. Глушковым. Подробно язык регулярных выражений рассмотрен в [3, 4].
Пусть имеется автомат, установленный в начальное состояние. На вход автомата подается произвольная последовательность букв. Если автомат среди этой последовательности букв находит «знакомое» слово, то он реагирует на него выдачей определенного выходного сигнала. Реакция автомата на промежуточные последовательности букв внутри слова не важна.
Видно, что данный язык удобно использовать только для описания ограниченного класса автоматов, а именно так называемых «распознающих» автоматов, поэтому в настоящее время язык регулярных выражений имеет ограниченное применение.
Пусть на вход автомата S, предварительно установленного в начальное состояние a0 Î A, поступает слово, составленное из символов входного алфавита X, которое вызывает на выходе автомата появление символа yi Î Y (рис. 6.1).
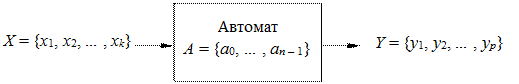 |
Рис. 6.1. Поступление на вход автомата слов входного алфавита
Алфавиты автомата определены следующим образом:
 A = {a0, a1, … , an – 1}
A = {a0, a1, … , an – 1}
X = {x1, x2, … , xk} . (6.1)
Y = {y1, y2, … , yp}
Входные слова, на которые автомат откликается выходным символом yi, можно объединить во множество Hi (x1, x2, … , xk). Это множество называется событием, представленным в автомате S выходным символом (буквой) yi.
Слово – конечная последовательность символов, принадлежащих некоторому множеству символов (алфавиту автомата). Если, например, алфавит Y содержит три символа y1, y2, y3, т. е.
Y = {y1, y2, y3}, (6.2)
то возможны слова y1, y1y1y1, y2y1, y3y3y2y1y2, y3, y3y1y2y1 и т. д.
Пустое слово – слово нулевой длины. Пустое слово принято обозначать буквой e. Для любого слова d выполняется соотношение ed = de = d. Считается, что пустое слово принадлежит любому алфавиту символов. Наличие пустого слова на входе автомата означает отсутствие входных сигналов.
Событие – произвольное множество слов конечной длины, составленных из букв входного алфавита X. В дальнейшем событие будем обозначать буквой H.
Элементарное событие во входном алфавите X – это какое-либо из (k + 1)-го элементарных событий x1, x2, … , xk, e, где e – пустое слово
X = {x1, x2, … , xk}. (6.3)
События называют пересекающимися, если они имеют общие слова, и непересекающимися, если таких слов нет. При абстрактном синтезе цифровых автоматов рассматриваются только непересекающиеся события, для которых выполняется условие однозначности выходной функции автомата.
Полностью определенный автомат можно задать таблицей, устанавливающей соответствие между попарно непересекающимися событиями
Hi(x1, x2, … , xk) и выходными символами y1, … , yi, … , yp (табл. 6.1). Аналогичную таблицу для частичного (не полностью определенного) автомата необходимо дополнить событием Hзапрзапрещенных входных слов (табл. 6.2).
| Таблица 6.1 Таблица событий полностью определенного автомата, представленных выходными буквами y1, y2, … , yp | Таблица 6.2 Таблица событий частичного автомата, представленных выходными буквами y1, y2, … , yp | |||
| Событие | Буква выходного алфавита | Событие | Буква выходного алфавита | |
| H1(x1, x2, … , xk) | y1 | H1(x1, x2, … , xk) | y1 | |
| H2(x1, x2, … , xk) | y2 | H2(x1, x2, … , xk) | y2 | |
| ¼ | ¼ | ¼ | ¼ | |
| Hp(x1, x2, … , xk) | yp | Hp(x1, x2, … , xk) | yp | |
| Hзапр(x1, x2, … , xk) | Не определена |
Конкатенацией (склеиванием) двух слов H1 и H2 называется слово H, которое получается в результате непосредственного слияния слова H1, стоящего слева, и слова H2, стоящего справа. Например, если
H1 = x1x2x5; (6.4)
H2 = x4x3x4, (6.5)
то конкатенация H1 и H2 – это слово:
H = x1x2x5x4x3x4, (6.6)
а конкатенация H2 и H1– это слово:
H = x4x3x4x1x2x5. (6.7)
Хотя операция конкатенации сходна с формой записи конъюнкции, это не одно и то же, конкатенация не подразумевает каких-либо логических операций.
Итерацией события H называется событие [H], состоящее из пустого слова e и всех слов вида H, HH, HHH и т. д. до бесконечности. Итерация пустого события равна пустому событию: [e] = e. Итерация события H определяется так:
[H] = [e] Ú H Ú HH Ú HHH Ú ¼ (6.8)
Регулярное событие может быть задано регулярным выражением, т. е. формулой, содержащей символы e, символы входного алфавита и знаки регулярных операций над ними. Одно и то же регулярное событие может быть представлено разными эквивалентными регулярными выражениями. Для этого используются тождественные соотношения алгебры событий, которыми можно пользоваться при преобразованиях и упрощениях формул [4].
Доказано, что любые регулярные выражения, и только они могут быть реализованы конечным автоматом. Справедливо и обратное утверждение: любой конечный автомат реализует лишь те алгоритмы, которые можно записать в виде регулярных выражений.
Регулярные выражения позволяют построить отмеченную таблицу состояний автомата Мура по методике, изложенной в [4]. В общих чертах идею перехода от регулярных выражений к табличному заданию автомата можно пояснить следующим образом. Множество событий связано с множеством выходных сигналов. Выходные сигналы автомата Мура зависят только от состояний автомата. Поэтому каждому выходному сигналу из множества выходных сигналов Y в автомате Мура можно поставить в соответствие конкретное состояние автомата Мура. Различные подмножества множества событий, которые не представляют ни одно из событий, можно считать пустым множеством событий. Если множество событий пусто, то автомат выдает пустое выходное слово e. Таким образом, если ни одно событие не наступило, автомат не выдает ни одного сигнала из множества выходных сигналов Y.
Таким образом, если получено регулярное выражение, от него можно перейти к заданию автомата на стандартном автоматном языке, т. е. при помощи таблицы.
Дата добавления: 2017-09-19; просмотров: 582;
