Описание абстрактного автомата при помощи функций переходов и функций выходов.

Представление автомата в виде «черного ящика». Математическое описание автомата

В абстрактной теории автоматов абстрагируются от способов кодирования входных/выходных сигналов и состояний и представляют их в виде букв. Цифровой автомат при этом представляют в виде «черного ящика» с одним входом и одним выходом (рис. 1.3).

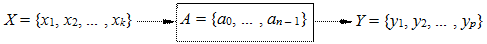Рис. 1.3. Абстрактный автомат в виде «черного ящика»

Любой автомат в общем виде описывается при помощи следующих множеств [1, 2]:

– множество входных сигналов Х;

– множество выходных сигналов Y;

– множество состояний А;

– функция переходов d;

– функция выходов λ;

– начальное состояние а₀.

В каждый момент дискретного времени на вход автомата поступает входной сигнал (буква входного алфавита), автомат переходит из одного состояния в другое (в частном случае автомат может не изменять своего состояния) и формирует выходной сигнал (одну из букв выходного алфавита). Алфавитом называется совокупность всех возможных входных сигналов. Произвольная совокупность букв алфавита называется словом. Слово может быть любой длины, в том числе нулевой, и содержать любую последовательность букв, в отличие от слов алфавитов естественных
языков.

Таким образом, в общем виде автомат описывается выражением:

S = (X, Y, A, δ, λ, a₀). (1.3)

Такой автомат называют инициальным. Автомат, который описывается выражением вида

S₁ = (X, Y, A, δ, λ), (1.4)

называют неинициальным, т. е. он может начать работать с любого состояния. Примером такого автомата может быть делитель частоты.

Автомат, который описывается выражением вида

S₂ = (X, Y, λ), (1.5)

описывает комбинационную схему.

В теории автоматов используется понятие «отображение». Например, запись f: X → Y означает, что функция f является отображением множества Х во множество Y. Для S₂ имеем: λ: X → Y.

Кроме того, в теории автоматов используется понятие «прямое произведение множеств», а также понятие «кортеж» – упорядоченная совокупность элементов множества. Прямое произведение двух множеств – это кортеж, состоящий из множества пар, в которых первый элемент принадлежит первому множеству, а второй элемент – второму множеству.

Рассмотрим пример.

Пусть даны два множества: X = {x₁, x₂}, A = {a₁, a₂}.

Получим прямое произведение этих множеств:

A × Y = {(a₁, x₁), (a₁, x₂), (a₂, x₁), (a₂, x₂)}; (1.6)

X × A = {(x₁, a₁), (x₁, a₂), (x₂, a₁), (x₂, a₂)}. (1.7)

Функция переходов δ определяется как отображение прямого произведения A *X во множество А:

δ: (A × X) → A, (1.8)

т. е. каждой паре вида (a_i, x_j) соответствует состояние a_k: (a_i, x_j) → a_k.

Рассмотрим пример.

Пусть даны два множества:

X = {x₁, x₂}, A = {a₁, a₂}. (1.9)

ъ

Вычислим прямое произведение A × X и поставим каждой паре вида (a_i, x_j) из кортежа состояние a_k:

A = A × X = {(a₁, x₁), (a₁, x₂), (a₂, x₁), (a₂, x₂)} = {a₁, a₂, a₂, a₁}, (1.10)

при этом имеем следующие соответствия:

(a₁, x₁) « a₁; (a₂, x₁) « a₃; (a₁, x₂) « a₂; (a₂, x₂) « a₁. (1.11)

Функция переходов в любом автомате всегда зависит от состояний и входного сигнала.

Функция выходов λ – это отображение прямого произведения A × X во множество Y,

λ: (A *X) → Y, (1.12)

т. е. паре вида (a_i, x_j) соответствует выходной сигнал y_n: (a_i, x_j) → y_n.

Рассмотрим пример.

Пусть даны три множества:

X = {x₁, x₂}, A = {a₁, a₂}, Y = {y₁, y₂, y₃}. (1.13)

Вычислим прямое произведение A × X и поставим каждой паре вида (a_i, x_j) из кортежа выходной сигнал y_n:

Y = A × X = {(a₁, x₁), (a₁, x₂), (a₂, x₁), (a₂, x₂)} = {y₁, y₂, y₃, y₁}, (1.14)

при этом имеем следующие соответствия:

(a₁, x₁) « y₁; (a₂, x₁) « y₃; (a₁, x₂) « y₂; (a₂, x₂) « y₁. (1.15)

Функция выхода в частном случае может не зависеть от текущего входного сигнала.

В этом случае имеем:

λ: A → Y. (1.16)

Если функция переходов и функция выходов заданы на всех возможных парах вида (a_i, x_j), то такой автомат называется полностью определенным, в противном случае – частичным (частично определенным или не полностью определенным).

Если у частичного автомата не определена функция переходов хотя бы для одной пары (a_i, x_j), то для задания такого автомата необходимо указать множество запрещенных входных слов, т. е. последовательностей букв входного алфавита, которые переводят автомат в неопределенное состояние. Если у частичного автомата не определена только функция выходов, то запрещенные входные слова указывать не нужно.

Рассмотрим пример.

Пусть задан автомат S₀:

X = {x₁, x₂}; A = {a₁, a₂, a₃}; Y = {y₁, y₂, y₃}; (1.17)

δ: (A × X) → A = {(a₁, x₁), (a₁, x₂), (a₂, x₁), (a₃, x₁), (a₃, x₂)} =

= {a₁, a₂, a₃, a₃, a₁}; (1.18)

λ: (A × X) → Y = {(a₁, x₁), (a₁, x₂), (a₂, x₁), (a₃, x₁), (a₃, x₂)} =

= {y₁, y₂, y₃, y₃, y₁}. (1.19)

Данный автомат является частичным, т. к. при (a₂, x₂), функция перехода не определена. Слова x₂x₂, x₁x₂x₂, x₁x₁x₂x₂, x₁x₁ … x₁x₂x₂ являются запрещенными, если автомат установлен в состояние а₁.

Пусть для автомата S₁, определенного на тех же множествах X, Y, A, функции переходов и выходов имеют вид:

δ: (A *X) → A = {(a₁, x₁), (a₁, x₂), (a₂, x₁), (a₂, x₂), (a₃, x₁), (a₃, x₂)} =

= {a₁, a₂, a₃, a₁, a₃, a₁}; (1.20)

λ: (A *X) → Y = {(a₁, x₁), (a₂, x₁), (a₂, x₂), (a₃, x₁)} = {y₁, y₁, y₂, y₃}. (1.21)

Для этого автомата функция перехода определена полностью, поэтому запрещенные входные слова указывать не нужно.

Пусть автоматы относятся к одному классу и установлены в начальное состояние, тогда полностью определенные автоматы эквивалентны, если при подаче на их входы одинаковых слов любой длины автоматы выдают на выходе одинаковые слова; частичные автоматы эквивалентны, если при подаче на их входы слов, не являющихся запрещенными, выдают на выходе одинаковые слова.

Автомат называется детерминированным, если он, находясь в одном и том же состоянии, под действием одного и того же сигнала совершает переход в одно и то же состояние. В противном случае автомат называется недетерминированным. Будем рассматривать только детерминированные автоматы.

6.23 Начальные автоматные языки