Реализация переключательных функций на мультиплексорах и ДЕШИФРАТОРАХ
Пусть требуется реализовать ПФ, зависящую от двух переменных и представленную таблицей истинности (таблица 1).
Таблица 1
| № набора | X1 | X0 | y |
В общем случае можно сформулировать следующее правило: если количество логических переменных n, от которых зависит реализуемая ПФ, совпадает с разрядностью адресной части мультиплексора, то эти переменные подаются на адресные входы мультиплексора (старшая переменная – на старший адресный вход), а на информационные входы мультиплексора с четырьмя входами – константы 0 и 1 в соответствии с таблицей истинности реализуемой ПФ (рисунок 1).
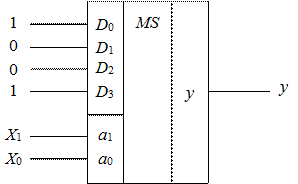 |
Рисунок 1. – Реализация ПФ yMS на мультиплексоре
Попробуем реализовать теперь ПФ, зависящую от трех переменных (см. таблицу 2), на том же мультиплексоре с четырьмя входами.
Для общего случая можно сформулировать следующее правило: если количество логических переменных n, от которых зависит реализуемая ПФ, на единицу больше разрядности адресной части мультиплексора, то данную ПФ можно реализовать на мультиплексоре с четырьмя входами и одном инверторе.
Таблица 2
| № набора | X2 | X1 | X0 | y |
Если в таблице 2 выделить четыре группы по две строки в каждой и отделить переменную Х0 от Х2 и Х1 , то получим таблицу 3 (где выделения сделаны двойной линией).
Таблица 3.3
| № набора | X2 | X1 | X0 | y | y = f(Х0) y = |
| X0 | |||||
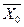
| |||||
Из таблицы 3 видно, что переменные Х2 и Х1 образуют четыре набора, на каждом из которых функция y зависит только от одной переменной Х0, причем значения y = f(Х0) легко выявляются из этой таблицы.
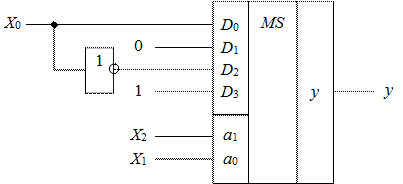 |
Рисунок 2. – Реализация ПФ 3 аргументов на мультиплексоре с четырьмя входами
Для реализации ПФ на дешифраторе используется свойство дешифратора с n адресными входами, согласно которому каждый из его m = 2n выходов реализует инвертированную конституенту «1» для каждого из m наборов аргументов (сигналов на адресных входах).
Пусть требуется реализовать ПФ, зависящую от трех переменных и представленную картой Вейча (см. рис. 1.5).
Рис. 1.5 Задание ПФ y картой Вейча
Эту функцию можно представить в СДНФ (1.7), в базисе И-НЕ (1.8), и в СКНФ (1.9), в базисе ИЛИ-НЕ(1.10):
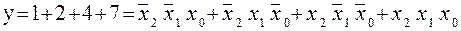 (1.7)
(1.7)
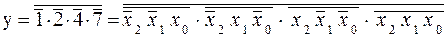 (1.8)
(1.8)
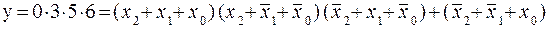 (1.9)
(1.9)
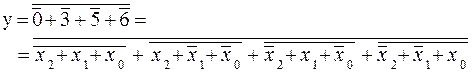 (1.10)
(1.10)
Поскольку в полном дешифраторе реализуются все конституенты, то для получения ПФ достаточно добавить к нему один логический элемент. Итак, для реализации ПФ по уравнению (1.7) требуется дешифратор с активной единицей выхода и четырехвходовый элемент ИЛИ (рис. 1.6); по уравнению (1.8) требуется дешифратор с активным нулем выхода и четырехвходовый элемент И-НЕ (рис. 1.7,); по уравнению (1.9) - дешифратор с активным нулем выхода и четырехвходовый элемент И (рис. 1.7) и по уравнению (1.10) - дешифратор с активной единицей выхода и четырехвходовый элемент ИЛИ-НЕ (рис. 1.8).
Из рассмотренного примера следует, что для реализации произвольной ПФ, зависящей от n переменных, требуются две ИС: дешифратор «1 из 2n» и логический элемент с числом входов не более 2n - 1.
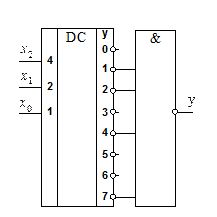
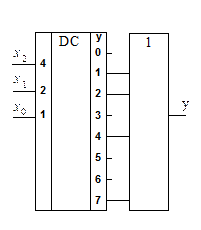
Рис. 1.6. Реализация ПФ по (1.7) Рис. 1.7. Реализация ПФ по (1.8)
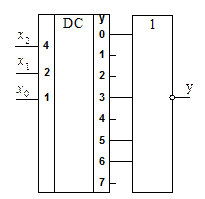
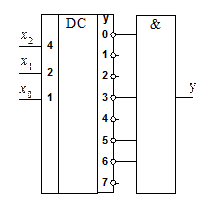
Рис. 1.8. Реализация ПФ по (1.9) Рис. 1.9. Реализация ПФ по (1.10)
4.15 Счетчики на D- и JK-триггерах
Дата добавления: 2017-09-19; просмотров: 1437;
