Реализация переключательных функций на логических элементах

Для синтеза электрической схемы для реализации ПФ по выражению для МДНФ с использованием логических элементов необходимо:

1) выбрать элементную базу;

2) определить необходимое число логических элементов;

3) определить необходимые электрические соединения;

4) проверить допустимую гальваническую нагрузку на выход каждого элемента (согласование по токовой и по емкостной нагрузке);

5) разработать электрическую принципиальную схему.

При синтезе ПФ на универсальных лабораторных стендах можно использовать элементы И, ИЛИ, И-НЕ, И-ИЛИ-НЕ.

Рассмотрим варианты реализации ПФ, заданной выражением (1):

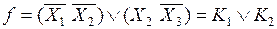. (1)

Реализуем ПФ на элементах И и ИЛИ. Для реализации ПФ на элементах И и ИЛИ нужно определить число входов элемента ИЛИ, а также сколько элементов И с требуемым числом входов нужно использовать.

Число входов элемента ИЛИ равняется числу конъюнкций в выражении для ПФ. Число элементов И равняется числу конъюнкций, состоящих из более чем одного аргумента. Число входов каждого из элементов И определяется числом аргументов в конъюнкции, реализуемой этим элементом. В нашем примере нужен элемент ИЛИ с двумя входами, 2 элемента И с двумя входами каждый (рисунок 1).

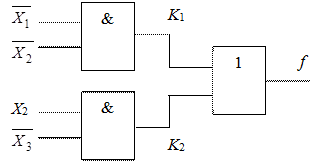Рисунок 1. – Реализация ПФ (1) на элементах И и ИЛИ

Данный способ реализации неудобен, т. к. для реализации ПФ необходимы различные логические элементы, не образующие универсальный базис, а элементы ИЛИ с большим числом входов не выпускаются. Такой способ построения схемы реализован в микросхемах ПЛМ.

При использовании универсального базиса И-НЕ необходимо перейти от задания ПФ при помощи МДНФ к заданию ПФ в базисе Шеффера. Для этого используется следующая последовательность действий:

- в выражении для МДНФ все конъюнкции заключаются в скобки;

- все операции конъюнкции и дизъюнкции заменяются на штрих Шеффера (И-НЕ);

- если конъюнкция образована только одной переменной, то эта переменная подвергается инверсии.

Проиллюстрируем эту последовательность действий примером, взяв за основу выражение (1):

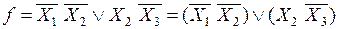, (2)

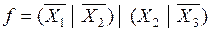. (3 )

Конъюнкции, образованные одной переменной, отсутствуют, поэтому данное выражение является исходным для реализации схемы (рисунок 2).

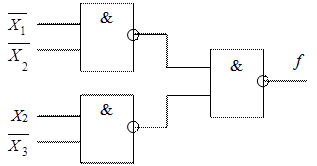Рисунок 2 – Реализация ПФ (3.3) на элементах И-НЕ

Для реализации ПФ на элементах И-НЕ нужно определить, сколько элементов И-НЕ с требуемым числом входов нужно использовать. При этом схема будет состоять из двух ступеней.

На первой ступени располагаются элементы И-НЕ, реализующие слагаемые дизъюнкции, число этих элементов равняется числу дизъюнктивных слагаемых, состоящих более чем из одного аргумента. Число входов каждого из элементов И-НЕ определяется числом аргументов в дизъюнктивном слагаемом, реализуемым этим элементом.

На второй ступени располагается элемент И-НЕ, реализующий на своем выходе значение ПФ. Число его входов равняется числу дизъюнктивных слагаемых.

В нашем примере для реализации 1-й ступени нужны 2 элемента
И-НЕ с двумя входами каждый, для реализации 2-й ступени нужен 1 элемент И-НЕ с двумя входами (см. рисунок 2).

Пусть выражение для МДНФ ПФ y имеет вид:

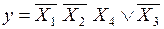. (4)

Перейдем к базису Шеффера:

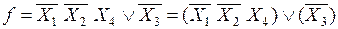, (5)

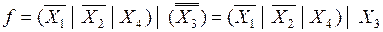. (6)

В нашем примере для реализации 1-й ступени нужен 1 элемент И-НЕ с тремя входами, для реализации 2-й ступени нужен 1 элемент И-НЕ с двумя входами (рисунок 3 ).

Рисунок 3. – Реализация ПФ (5) на элементах И-НЕ

ПФ можно реализовать в базисе И-ИЛИ-НЕ. Задача синтеза переключательной функции f (X_{n – 1}, X_{n – 2}, …, X₁, X₀) n аргументов X_{n – 1}, … , X₁, X₀ на основе логических элементах типа И-ИЛИ-НЕ сводится к поиску минимальной дизъюнктивной нормальной формы функции 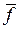(X_{n – 1},
X_{n – 2},…, X₁, X₀), инверсной по отношению к заданной функции. Основанием для этого служит формула двойного отрицания:

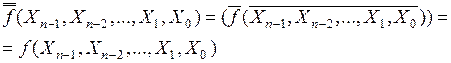. (7)

Из (7) следует, что математическое выражение для функции f можно представить как инверсию выражения для .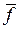

Последовательность синтеза с применением карт Вейча следующая.

Заполняется карта Вейча или карта Карно для функции f. Далее заполняется карта Вейча или карта Карно для функции 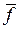следующим образом:

- если в клетке карты Вейча для функции f записана «1», то в аналогичной клетке карты для 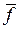нужно записать «0»;

- если в клетке карты Вейча для функции f записан «0», то в аналогичной клетке карты для 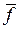нужно записать «1»;

- если в клетке карты Вейча для функции f записан «прочерк» (ПФ не определена), то нужно записать «прочерк».

Для функции 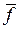по карте Вейча или карте Карно найти минимальную дизъюнктивную нормальную форму (МДНФ).

Проинвертировать левую и правую части выражения для 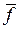, поставив знак инверсии над 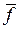и над выражением для МДНФ.

В соответствии с формулой двойного отрицания заменить 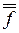на f.

Рассмотрим пример.

Синтезировать на элементах И-ИЛИ-НЕ не полностью определенную переключательную функцию f четырех аргументов, заданную МДНФ для переключательной функции :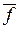

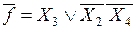. (8)

Проинвертируем левую и правую части выражения для 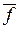, поставив знак инверсии над 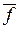и над выражением для МДНФ:

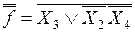. (9)

Схема реализации переключательной функции f на элементе
И-ИЛИ-НЕ универсального лабораторного стенда УМ 11 изображена на рисунке 4.

Рисунок 4. – Реализация ПФ (8) на элементе 3-2И-3И-ИЛИ-НЕ