Фильтрация случайных сигналов в ЛДС

6.2.1.1. Основные понятия случайных дискретных сигналов

Стационарный случайный дискретный процесс характеризуется математическим ожиданием и автокорреляционной функцией:

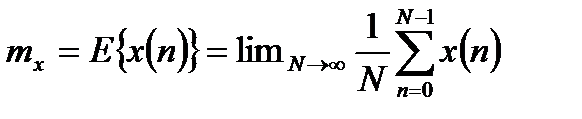, (1.1)

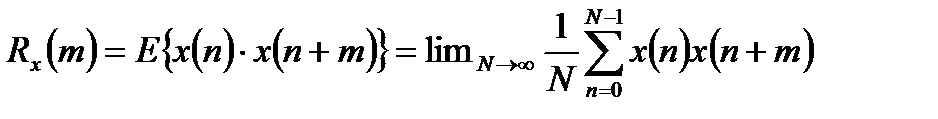, (1.2)

где 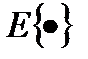- усреднение по времени или ансамблю (для эргодических сигналов).

Если анализируется только случайного сигнала от среднего значения, рассматривают автоковариационную функцию:

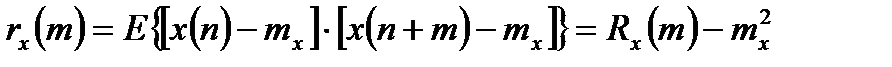. (1.3)

В случае 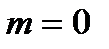автоковариационная функция дает дисперсию сигнала:

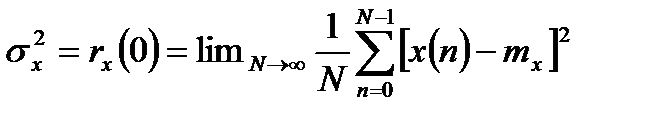. (1.4)

Степень линейной связанности двух различных случайных дискретных сигналов определяется взаимной корреляционной и взаимной ковариационной функцией:

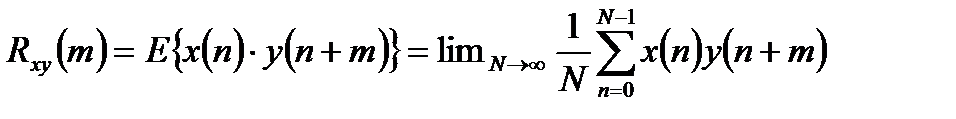, (1.5)

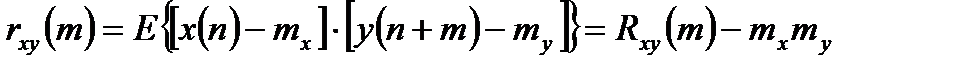. (1.6)

Два случайных сигнала называются некоррелированными, если:

.

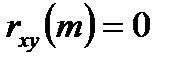Дискретный белый шум 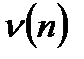отличается от других случайных дискретных сигналов тем, что его текущее значение не зависит от предшествующих значений. Нормальный дискретный белый шум полностью характеризуется дтематическим ожиданием 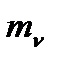и ковариационной функцией:

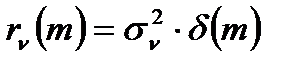, (1.7)

где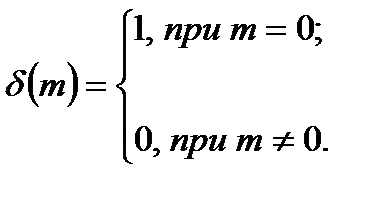

В отличие от аналогового белого шума, дисперсия дискретного белого шума не является бесконечной и такой шум является физически реализуемым.

6.2.1.2. Прохождение случайных сигналов через ЛДС

Во временной области необходимо учитывать связь вход-выход ЛДС с импульсной характеристикой 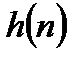по формуле свертки:

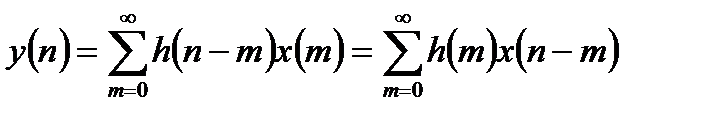. (1.8)

Взяв математическое ожидание от уравнения свертки, можно получить выражение для математического ожидания выходного сигнала ЛДС:

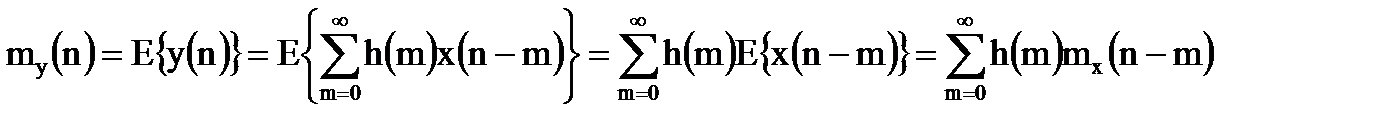. (1.9)

Таким образом, математическое ожидание выходного сигнала получается в результате подачи на вход ЛДС математического ожидания входного сигнала .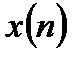

Автокорреляционная функция выходного сигнала ЛДС определяется выражением:

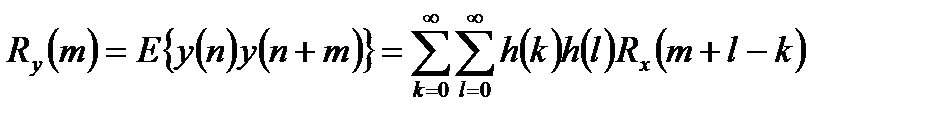. (1.10)

Соответственно, для средней мощности выходного сигнала можно получить:

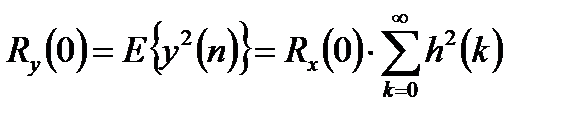. (1.11)

Если входной сигнал имеет нулевое среднее значение, можно получить:

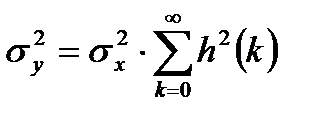. (1.12)

Соответственно можно получить для автоковариационной функции выходного сигнала:

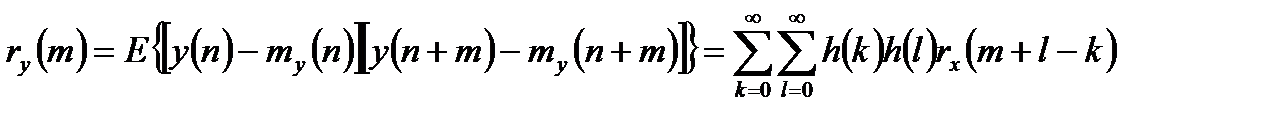. (1.13)

Для взаимной ковариационной функции входного и выходного сигналов в случае нулевых средних можно записать:

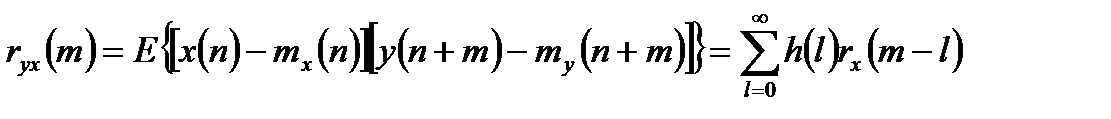. (1.14)