Способ расчета размерных цепей на максимум-минимум

Чтобы обеспечить полную взаимозаменяемость, необходимо даже при самых неблагоприятных сочетаниях размеров составляющих звеньев получить размер замыкающего звена в заданных пределах. Этот принцип лежит в основе метода расчета на максимум-минимум.

В общем случае номинальный размер замыкающего линейного звена можно определить по формуле:

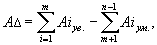
(14.1.)

где 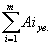- сумма номинальных размеров увеличивающих звеньев;

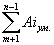- сумма номинальных размеров уменьшающих звеньев;

m - число увеличивающих звеньев;

n - общее число звеньев размерной цепи.

Запишем выражения максимального и минимального значений замыкающего звена:

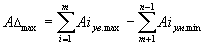
	(14.2.)
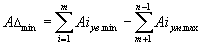
	(14.3.)

Вычитая из первого равенства второе и перегруппировав члены правой части с их знаками, получим:

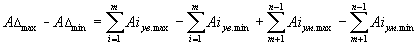
(14.4.)

Т.к. разность предельных размеров есть допуск, то можно записать:

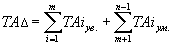
(14.5.)

или

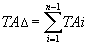
(14.6.)

т.е. допуск замыкающего звена равен сумме допусков всех составляющих звеньев.

Верхнее и нижнее отклонения звена А_i размерной цепи принято обозначать Es (A_i) и Ei (A_i) соответственно. Координаты середины поля допуска обозначаются Ec (A_i).

Для определения отклонений замыкающего звена выразим предельные размеры в виде алгебраической суммы номинального размера и предельного отклонения:

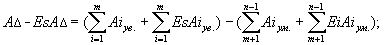
	(14.7.)
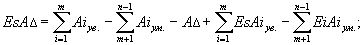
	(14.8.)

Так, как первые три члена правой части вместе равны ), что следует из общего уравнения размерной цепи, получаем:

	(14.9.)
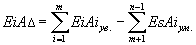
	(14.10.)

Эти равенства можно записать, выразив предельные отклонения через координату середины поля допуска замыкающего звена:

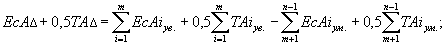
	(14.11.)
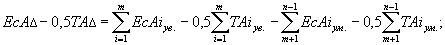
	(14.12.)

Сложив последние уравнения и разделив их на 2, получим выражение для определения координаты середины поля допуска замыкающего звена:

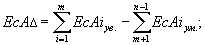
(14.13.)

Таким образом, мы получили все уравнения, необходимые для решения обратной задачи.

Более сложной является прямая задача, когда по известному допуску и отклонениям замыкающего звена требуется найти допуски и отклонения всех составляющих звеньев. Эту задачу можно решать двумя способами:

- способом равных допусков;

- способом назначения допусков одного квалитета.

Способ равных допусков применяют, если составляющие размеры имеют один порядок (например, входят в один интервал диаметров) и могут быть выполнены с примерно одинаковой экономической точностью. В этом случае можно условно принять:

ТА₁ = ТА₂ = . . . = ТА_n-1,

откуда

т.е. допуск любого составляющего звена равен допуску замыкающего звена, деленному на число составляющих звеньев.

Этот способ прост, но недостаточно точен. Его можно рекомендовать только для предварительного назначения допусков составляющих размеров.

Способ допусков одного квалитета применяют, если все составляющие размерную цепь размеры могут быть выполнены с допуском одного квалитета и допуски составляющих размеров зависят от их номинального значения. Для выполнения этого условия надо допуск замыкающего звена разделить пропорционально единице допуска каждого составляющего звена. Допуск звена равен:

ТАi = ai_Ai

Подставив это значение допуска в выражение

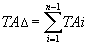
получим

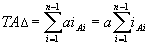
Так как мы назначаем допуски одного квалитета, число единиц допуска у всех звеньев должно быть одинаковым, отсюда:

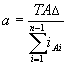
(14.15.)

По значению а выбирают ближайший квалитет, по которому необходимо назначить допуски на все звенья.

Если коэффициент точности а не подходит близко ни к одному квалитету, а имеет какое-то среднее значение, можно на часть звеньев, более сложных в изготовлении, назначить допуски по ближайшему грубому квалитету, а на остальные звенья - по более точному. При этом должно соблюдаться условие:

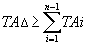
(14.16.)

Найдя допуски ТА₁, ТА₂ ... ТА_n-1 по заданным отклонениям Es (AD ) и Ei (AD ) определяют значения и знаки верхних и нижних отклонений составляющих размеров так, чтобы они удовлетворяли уравнения (14.9.) и (14.10.). Если эти условия не соблюдаются, корректируют отклонения.