Законы сохранения количества движения
Законы сохранения количества движения системы получаются как частные случаи теоремы об изменении количества движения для системы в зависимости от особенностей системы внешних сил, приложенных к рассматриваемой механической системе, а для одной точки – от особенностей сил, действующих на точку. Внутренние силы при этом могут быть любыми, так как они явно не влияют на изменение количества движения системы.
Возможны два частных случая:
1. Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т. е. 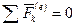 , то из теоремы об изменении количества движения системы, например в форме (68), следует, что
, то из теоремы об изменении количества движения системы, например в форме (68), следует, что
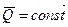 . (166)
. (166)
Этот закон (точнее, частный случай теоремы) формулируется так: если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению. В проекциях на координатные оси, по этому закону,
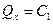 ,
, 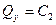 ,
, 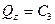 . (166')
. (166')
где 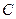 – постоянные величины.
– постоянные величины.
2. Если равна нулю проекция главного вектора внешних сил на какую-либо координатную ось 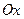 , т.е.
, т.е. 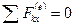 , то из (163') имеем
, то из (163') имеем
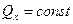 . (167)
. (167)
Выражение (167) является законом сохранения проекции количества движения системы: если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю, то проекция количества движения на ту же ось является постоянной величиной.
Дата добавления: 2017-09-19; просмотров: 357;
