Теорема о движении центра масс

Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к механической системе:

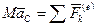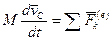, или , (155)

где 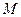– масса системы, 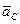– ускорение центра масс, 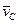– скорость центра масс.

Проецируя (155) на прямоугольные декартовы оси координат, получаем дифференциальные уравнения движения центра масс:

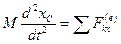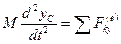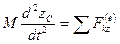, , . (155')

где 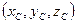– координаты центра масс.

Из теоремы о движении центра масс системы получаются дифференциальные уравнения поступательного движения твердого тела: при поступательном движении твердого тела ускорения всех точек тела одинаковы по модулю и направлению, т.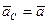е. , где 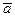– ускорение произвольной точки тела. Учитывая это, из теоремы о движении центра масс получаем следующее дифференциальное уравнение поступательного движения тела в векторной форме:

.

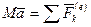Проецируя на оси координат, имеем:

, , .

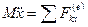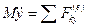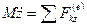Это дифференциальные уравнение поступательного движения тела в проекциях на прямоугольные оси координат. В этих уравнениях 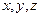являются координатами произвольной точки тела. Тело, совершающее поступательное движение, имеет три степени свободы, поэтому можно составить три дифференциальных уравнения его движения.