Тонкое кольцо (круглое колесо)
Имеем тонкое кольцо радиусом 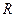 и массой
и массой 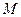 , распределенной по его ободу. Оси координат
, распределенной по его ободу. Оси координат 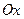 и
и 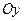 расположим в плоскости кольца. Момент инерции
расположим в плоскости кольца. Момент инерции 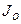 относительно его центра
относительно его центра 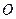 совпадает с моментом инерции
совпадает с моментом инерции 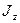 относительно координатной оси
относительно координатной оси 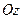 , перпендикулярной плоскости кольца.
, перпендикулярной плоскости кольца.
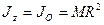 ,
, 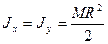 . (150)
. (150)
Круглый цилиндр
Для круглого однородного цилиндра, масса которого 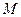 , радиус
, радиус 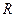 и длина
и длина 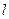 , его моменты инерции относительно продольной оси симметрии
, его моменты инерции относительно продольной оси симметрии 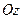 и относительно его поперечной оси симметрии
и относительно его поперечной оси симметрии 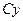 равны:
равны:
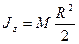 ,
, 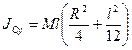 . (151)
. (151)
Шар
Пусть масса шара 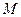 , радиус
, радиус 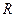 . Моменты инерции шара относительно осей координат и центра шара
. Моменты инерции шара относительно осей координат и центра шара 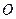 равны:
равны:
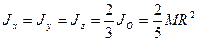 . (152)
. (152)
ЛЕКЦИЯ № 7
Теоремы динамики
Внешними силами механической системы называются силы, с которыми действуют на точки системы тела и точки, не входящие в рассматриваемую систему.
Внутренними силами механической системы называют силы взаимодействия между точками рассматриваемой системы.
Внешнюю силу, приложенную к какой-либо точке системы, обозначим 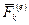 , а внутреннюю –
, а внутреннюю – 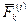 . Внутренние и внешние силы могут включать в себя как активные силы, так и силы реакций связей.
. Внутренние и внешние силы могут включать в себя как активные силы, так и силы реакций связей.
Главный вектор всех внутренних сил системы и главный момент этих сил относительно произвольной точки равны нулю при любом состоянии системы, т. е. при ее равновесии и при произвольном движении.
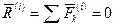 ,
, 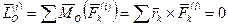 . (153)
. (153)
Если рассмотреть какие-либо две произвольные точки системы, например 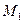 и
и 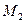 , то для них
, то для них 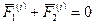 , так как силы действия и противодействия всегда равны друг другу по модулю, противоположны по направлению и действуют вдоль одной прямой линии, соединяющей взаимодействующие точки. Главный вектор внутренних сил
, так как силы действия и противодействия всегда равны друг другу по модулю, противоположны по направлению и действуют вдоль одной прямой линии, соединяющей взаимодействующие точки. Главный вектор внутренних сил 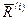 состоит из векторной суммы таких сил действия и противодействия, так как вся система состоит из пар взаимодействующих точек. Следовательно, он равен нулю. Так как обе силы имеют одинаковые плечи и противоположные направления векторных моментов, их главный вектор равен нулю. Главный момент внутренних сил
состоит из векторной суммы таких сил действия и противодействия, так как вся система состоит из пар взаимодействующих точек. Следовательно, он равен нулю. Так как обе силы имеют одинаковые плечи и противоположные направления векторных моментов, их главный вектор равен нулю. Главный момент внутренних сил 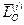 состоит из векторной суммы таких выражений, равных нулю.
состоит из векторной суммы таких выражений, равных нулю.
Пусть даны внешние и внутренние силы, действующие на систему, состоящую из 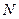 точек. Если к каждой точке системы приложить равнодействующую силу внешних сил
точек. Если к каждой точке системы приложить равнодействующую силу внешних сил 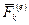 и равнодействующую силу всех внутренних сил
и равнодействующую силу всех внутренних сил 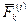 то для любой
то для любой 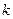 -й точки системы можно составить дифференциальное уравнение движения, например, в векторной форме, т. е.
-й точки системы можно составить дифференциальное уравнение движения, например, в векторной форме, т. е.
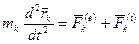 , (
, ( 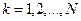 ). (154)
). (154)
Систему 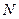 дифференциальных уравнений (154) называют дифференциальными уравнениями движения механической системы в векторной форме. Если спроецировать векторные дифференциальные уравнения (154) на прямоугольные декартовы оси координат, то получим систему
дифференциальных уравнений (154) называют дифференциальными уравнениями движения механической системы в векторной форме. Если спроецировать векторные дифференциальные уравнения (154) на прямоугольные декартовы оси координат, то получим систему 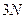 дифференциальных уравнений, описывающих движение точек механической системы.
дифференциальных уравнений, описывающих движение точек механической системы.
Дата добавления: 2017-09-19; просмотров: 414;
