Дифференциальные уравнения движения материальной точки
Используя основной закон динамики, можно получить дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей 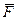 , а массу точки
, а массу точки 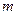 , получаем
, получаем
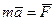 . (128)
. (128)
 Из кинематики точки известно, что ускорение
Из кинематики точки известно, что ускорение 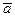 выражается через радиус-вектор
выражается через радиус-вектор 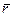 (рис. 48):
(рис. 48):
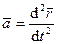 .
.
 Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
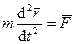 . (129)
. (129)
Если спроецировать обе части уравнений (128) или (129) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
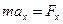 ,
, 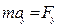 ,
, 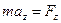 .
.
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
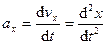 ;
; 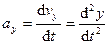 ,
, 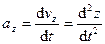 .
.
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имею вид
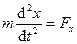 ,
, 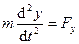 ,
, 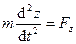 . (130)
. (130)
Дата добавления: 2017-09-19; просмотров: 678;
