Уравнение Аррениуса

Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.

Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.

Рассмотрим путь некоторой элементарной реакции

А + В ––> С

Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:

А ––> K^# ––> B

Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е'_А выше, нежели энергия активации прямой реакции E_A. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).

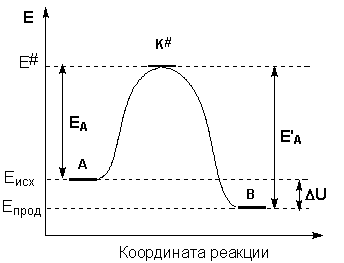
Рис. 2.5. Энергетическая диаграмма химической реакции. E_исх – средняя энергия частиц исходных веществ, E_прод – средняя энергия частиц продуктов реакции.

Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):

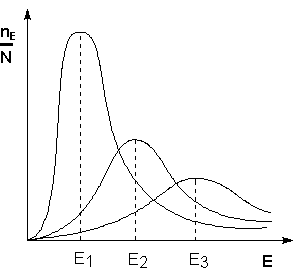
Рис. 2.6. Распределение частиц по энергии. Здесь nЕ/N - доля частиц, обладающих энергией E; E_i - средняя энергия частиц при температуре T_i (T₁ < T₂ < T₃).

Рассмотрим термодинамический вывод выражения, описывающего зависимость константы скорости реакции от температуры и величины энергии активации – уравнения Аррениуса. Согласно уравнению изобары Вант-Гоффа,

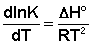(II.31)

Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:

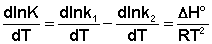(II.32)

Представив изменение энтальпии реакции ΔHº в виде разности двух величин E₁ и E₂, получаем:

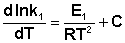(II.33)

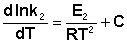(II.34)

Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где E_A – энергия активации:

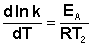(II.35)

После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:

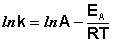(II.36)

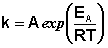(II.37)

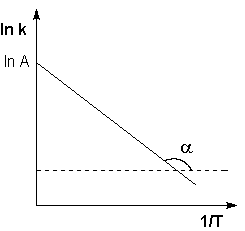
Рис. 2.7. Зависимость логарифма константы скорости химической реакции от обратной температуры.

Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации E_A и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).

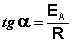(II.38)

Зная энергию активации реакции и константу скорости при какой-либо температуре T₁, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T₂:

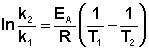(II.39)