ФОРМАЛЬНАЯ МОДЕЛЬ ОБЪЕКТА

Некоторое напоминание о математических понятиях:

Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и об­разующих в общем случае следующие подмножества:

совокупность входных воздействий на систему

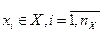, где n – число входных воздействий;

совокупность воздействий внешней среды

;

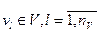совокупность внутренних (собственных) параметров системы

,

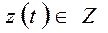которые являются независимыми (экзогенными) переменными и в векторной форме имеют вид:

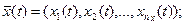
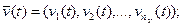
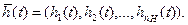
И совокупность выходных характеристик системы

,

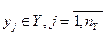которые являются зависимыми (эндогенными) переменными:

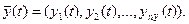
Процесс функционирования системы S описывается во времени оператором F_s, который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида

,

y(t)=F_s(x,v,h,t).

Совокупность зависимостей выходных характеристик системы от времени 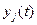для всех видов 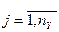, и_г называется выходной траек­торией 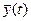.Зависимость (1) называется законом функционирова­ния системы S и обозначается F_s. В общем случае закон функци­онирования системы F_s может быть задан в виде функции, функци­онала, логических условий, в алгоритмической и табличной формах или в виде словесного правила соответствия.

алгоритма функционирования A_s, под которым понимается метод получения выходных характеристик с учетом входных воздействий 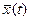, воздействий внешней среды 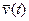и собственных параметров системы 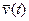. Динамические модели – это математические модели, описывающие поведение объекта системы во времени, т.е. отображающие его динамические свойства.

Для статических моделей математическая модель представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, Н], что в векторной форме может быть записано как

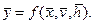
Соотношения параметров модели, выраженные в определенные моменты времени, называют состояниями (срезами). Состояние системы S характеризуется векторами:

;

,

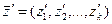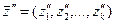где , ,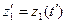

, ,

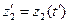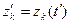
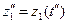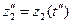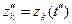
в момент , .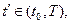

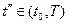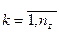Если рассматривать процесс функционирования системы S как последовательную смену состояний z₁(t), z₂(t), ..., z_k(t), то они могут быть интерпретированы как координаты точки в k-мерном фазовом пространстве, причем каждой реализации процесса буде соответствовать некоторая фазовая траектория. Совокупность все возможных значений состояний {z} называется пространством состояний объекта моделирования Z, причем z_k Î Z.

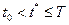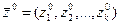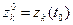Состояния системы S в момент времени полностью определяются начальными условиями , где ; входными воздействиями 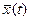; внутренними параметрами 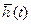и воздействиями внешней сре­ды 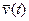, которые имели место за промежуток времени (t^* - t₀) с помощью двух векторных уравнени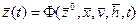й:

и ,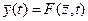

т.е. 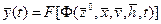(вход® состояние® выход).

Язык моделирования отличается от языка математики тем, что в языке математики состояние системы никого не интересует, т.е. вход® выход. В моделировании вход® состояние® выход, главное состояние.

В общем случае время в модели системы S может рассматриваться на интервале моделирования (0, T) как непрерывное, так и дискретное, т. е. квантованное на отрезки длиной Dt временных единиц каждый, когда T=mDt, где 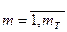— число интервалов дискретизации.

Таким образом, под математической моделью объекта (реаль­ной системы) понимают конечное подмножество переменных 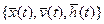вместе с математическими связями между ними и харак­теристиками .

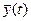Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями

Если учитываются стохастические воздействия внешней среды 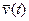и стохастические внутренние параметры 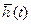, то это стохастическая модель.

Виды моделирования