ДИСКРЕТНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Р-СХЕМЫ)

Рассмотрим особенности построения математических схем при дискретно-стохастическом подходе к формализации процесса функционирования исследуемой системы S.Так как сущность дискретизации времени при этом подходе остается аналогичной конечным автоматам, то влияние фактора стохастичности проследим также на разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах.

Основные соотношения.В общем виде вероятностный автомат (англ, probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирова­ние которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.

Применение схем вероятностных автоматов (Р-схем) имеет важ­ное значение для разработки методов проектирования дискретных систем, проявляющих статистически закономерное случайное пове­дение, для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, а также для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.

Введем математическое понятие Р-автомата, используя поня­тия, введенные для F-автомата. Рассмотрим множество G, элемен­тами которого являются всевозможные пары (x_i, z_s), где x_i и z_s — элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции j и y, то с их помощью осуществляются отображения G®Z и G®Y, то говорят, что F =<Z, X, Y, j, y> определяет автомат детерминиро­ванного типа.

Введем в рассмотрение более общую математическую схему. Пусть Ф — множество всевозможных пар вида (z_k, y_j), где у_j — элемент выходного подмножества Y.Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:

При этом 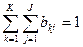, где b_kj — вероятности перехода автомата в состояние z_k и появления на выходе сигнала y_j, если он был в состоянии z_s,и на его вход в этот момент времени поступил сигнал x_i. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов P = <Z, X, Y, B> называ­ется вероятностным автоматом (P-автоматом).