Обработка РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ СИСТЕМ

Особенности получения результатов моделирования.информация о состояниях процесса функционирования исследуемых систем z(t)ÎZ. Эта информация является исходным материалом. Критерием оценки будем называть любой количественный показатель, по которому можно судить о результатах моделирования системы. В ходе машинного эксперимента изучается поведение модели на интервале времени [0, T].Поэтому критерий оценки является векторной случайной функцией:

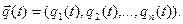
Рассмотрим общую схему фиксации и обработки результатов В общем случае критерием интерпретации результатов является случайный процесс 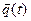, 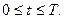Полагаем, что состояние проверяется каждые Dt временных единиц, При этом вычисляют значения 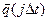, , 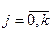критерия 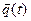. Таким образом, о свойствах случайного процесса 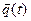судят по свойствам случайной последовательности 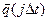, , 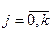или, иначе говоря, по свойствам m-мерного вектора вида

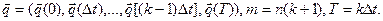
Процесс функционирования системы S на интервале [О, T] моделируется N-кратно с получением независимых реализаций 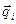, , 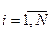вектора 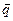.Работа модели на интервале [О, T] называется

Iºi; Jºj; Kºk; Nºn; Tºt; DTºDt; Qºq. В общем случае алгоритмы фиксации и ста­тистической обработки данных моделирования содержат три цикла. Полагаем, что имеется машинная модель М_м системы S.

Внутренний цикл (блоки 5 — 8)позволяет получить последовательность 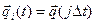, 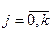в моменты времени t = 0, Dt, 2Dt, …, kDt = T. Основной блок 7 реализует процедуру вычисления последовательности 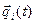^: ВЫЧ[QI(T)]. Именно в этом блоке имитируется процесс функционирования моделируемой системы S на интервале времени [О, T].

Промежуточный цикл (блоки 3 — 10), в котором организует­ся N-кратное повторение прогона модели, позволяющее судить об оценках характеристик варианта системы. Окончание моделирования варианта системы S может определяться не только заданным числом реализаций (блок 10), как это показано на схеме, но и заданной точностью результатов моделирования. В этом цикле содержится блок 9, реализующий процедуру фиксации результатов моделирования по i-му прогону модели 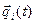: ФРМ [QI(T)].

Внешний цикл (блоки 1 — 12) охватывает оба предшествующих 1, 2, 11, 12, управляющие последовательностью моделирования вариантов системы S. Здесь организуется поиск оптимальных структур, алгоритмов и параметров системы S, т. е. блок 11 обрабатывает результаты моделирования исследуемого k-говарианта системы ОРМ [QK], блок 12 проверяет удовлетворительность полученных оценок характеристик процесса функционирования системы 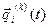, требуемым (ведет по­иск оптимального варианта системы ПОВ [S(K)]), блок 1 изменяет структуру, алгоритмы и параметры системы S на уровне ввода исходных данных для очередного k-говарианта системы ВИД [S (К)].Блок 13 реализует функцию выдачи результатов модели­рования по каждому k-му варианту модели системы S_k, т. е. ВРМ [QK].

Рассмотренная схема позволяет вести статистическую обработку результатов моделирования.

Если свойства моделируемой системы S определяются значением критерия 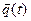в некоторый заданный момент времени, например в конце периода функционирования модели t = kDt = T, то обработка сводится к оценке распределения n-мерного вектора 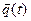по независимым реализациям 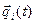, , 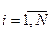полученным в результате N прогонов модели. Если в моделируемой системе S по истечению некоторого времени с начала работы t₀ = k₀Dt установится стационарный режим, то о нем можно судить по одной, достаточно длинной реализации 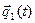критерия 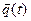, стационарного и эргодического на интервале [t₀, Т].Для рассмотренной схемы это означает, что исключается средний цикл (n=1) и добавляется оператор, позволяющий начать обработку значений 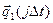при j ³ k₀.