ПОСТРОЕНИЕ КОНЦЕПТУАЛЬНЫХ МОДЕЛЕЙ СИСТЕМ И ИХ ФОРМАЛИЗАЦИЯ

На первом этапе машинного моделирования — построения концептуальной модели M_к системы S и ее формализации —назначением этого этапа является переход от содержательного описания объекта к его математической модели,. Наиболее ответственными являются проведение границы между системой S и внешней средой Е, упрощение описания системы и построение сначала концептуальной, а затем формальной модели системы. Модель должна быть адекватной (т.е отражает процесс ее функционирования во внешней среде Е).

Переход от описания к блочной модели. Наиболее рационально строить модель по блочному принципу. При этом могут быть выделены три автономные группы блоков. Блоки первой группы представляют собой имитатор воздействий внешней среды Е на систему S; блоки второй группы являются собственно моделью процесса функционирования исследуемой системы S; блоки третьей группы — вспомогательными и служат для машинной реализации, а также для фиксации и обработки результатов моделирования.

Рассмотрим механизм перехода от описания процесса функционирования некоторой гипотетической системы к модели этого процесса.

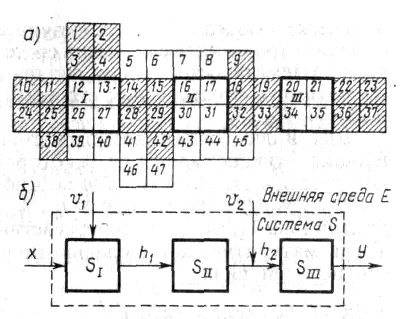
Рис.7. Модель системы: а — концептуальная; б — блочная

Эти квадраты описание подпроцессов Переход от описания системы к ее модели в этой интерпретации сводится к исключению из рассмотрения некоторых второстепенных элементов описания. Оставшиеся элементы системы S группируются в блоки S_I, S_II, S_III, отражающие процесс функционирования исследуемой системы. Поведение этих блоков должно быть хорошо изучено и для каждого из них построена математическая модель,. Построенная блочная модель процесса функционирования исследуемой системы S предназначена для анализа характеристик этого процесса, который может быть проведен при машинной реализации полученной модели.

Математические модели процессов. После перехода от описания моделируемой системы S к ее модели М_к, построенной по блочному принципу, необходимо построить математические модели процессов, происходящих в различных блоках. Математическая модель представляет собой совокупность соотношений, определяющих характеристики процесса входных воздействии x₁, x₂, ..., x_nX и воздействий внешней среды v₁, v₂, ..., v_nV. Тогда математической моделью процесса может служить система соотношений вида. Если бы функции f₁, f₂, ..., f_m были известны, то соотношения (1) оказались бы идеальной математической моделью процесса функционирования системы S.

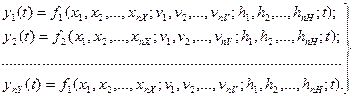(1)

Таким образом, на этой стадии сущность формализации подпроцессов будет состоять в подборе типовых математических схем. Содержательное описание является исходным материалом для последующих этапов формализации: построения формализованной схемы процесса функционирования системы и математической модели этого процесса. Для моделирования процесса функционирования системы на ЭВМ необходимо преобразовать математическую модель процесса в соответствующий моделирующий алгоритм и машинную программу.