МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Математическая модель (ММ) – это система математических соотношений, описывающих изучаемый процесс или явление. Это приближенное описание какого-либо класса явлений внешнего мира, выраженного с помощью математической символики.

В математических моделях объекта проектирования (ОП) обычно выделяют свойства систем, элементов систем и внешней среды, в которой должен действовать объект. Количественные представления этих свойств – параметры.

Различают:

1. Выходные параметры – как величины, характеризующие свойства системы;
2. Внешние параметры – как величины, характеризующие свойства внешней среды;
3. Внутренние параметры – как величины, характеризующие свойства элементов системы.

Для блока ЭВА выходные параметры: объем ОЗУ, время записи/считывания, число разрядов, и т.д.; внутренние параметры: скорость регенерации памяти, число и вид элементов, типа ОЗУ, и т.д.; внешние параметры: температура окружающей среды, напряжение питания, механические и климатические воздействия.

Если обозначить:

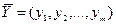- векторы выходных параметров;

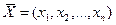- векторы внутренних параметров;

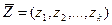- векторы внешних параметров,

то выражение 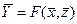- математическая модель, позволяющая определить выходной параметр 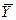в зависимости от параметров .

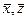В общем виде выражение 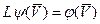- общий вид математической модели, где:

L – оператор;

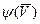- вектор фазовых переменных, характеризующий информационное или физическое состояние объекта;

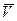- вектор независимых переменных;

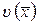- заданная функция независимых переменных.

Математическая модель представляет собой упрощение реальной ситуации и ее идеализацию.

Часто вначале рассматривается наиболее упрощенная модель поведения, явления, ситуации, после пристального изучения которой (в течение нескольких шагов) строится более сложная модель, учитывающая большее количество факторов и отношений.

В другом подходе, наоборот, сразу строят модель, охватывающую максимум факторов и отношений.

Рис. 1. Структура моделирования
2. Классификация математических моделей:

По характеру отражаемых свойств объекта:

- абстрактные;

- функциональные;

- структурные;

- технологические;

По отношению к иерархическому уровню:

- микроуровень;

- макроуровень;

- метауровень.

В зависимости от вида уравнений, используемых в моделях:

- линейные;

- нелинейные.

Хотя основные математические модели построены на основании линейных процессов и они с достаточной точностью описывают несложные явления, практика показала, что они не годятся для описания сложных явлений. Приходится переходить к нелинейным процессам, нелинейным описаниям.

В зависимости от наличия в моделях случайных параметров:

- статистические (вероятностные);

- детерминированные.

По способу представления свойств объекта:

- аналитические;

- алгоритмические;

- имитационные.

По виду представляемых параметров:

- аналоговые;

- дискретные.

По степени детализации описаний внутри определенного иерархического уровня:

- полные модели;

- макромодели.

Функциональные ММ отражают обычно в виде систем уравнений функционирования объекта.

Структурные ММ чаще всего отображают геометрические и топологические свойства объектов (топологические свойства дают в основном состав и взаимосвязи элементов).

Технологические ММ – модели организации технологических процессов в производстве.

Теоретические ММ получают на основе изучение физических закономерностей функционирования объектов проектирования, построения аналитических зависимостей, асимптотических оценок.

Эмпирические ММ строят на основе опыта специалистов высокой квалификации с учетом изучения внешних проявлений свойств объекта.

ММ на микроуровне чаще всего описывают физические процессы, протекающее в непрерывном производстве и времени с помощью ДУ в частных производных. Используют только в несложных элементах (механические напряжения, температурные поля, давления, и т.д.)

ММ на макро- и мета- уровне обычно составляются из систем ОДУ.

Полную ММ получают непосредственным объединением моделей в одну укрупненную систему.