Математические встроенные функции

В выражениях можно использовать следующие математические функции:

1) Тригонометрические (аргумент в радианах): sin(x), cos(x), tan(x)

2) Обратные тригонометрические (результат в радианах): asin(x), acos(x), atan(x)

3) Гиперболические: sinh(x), cosh(x), tanh(x)

4) Обратные гиперболические: asinh(x), acosh(x), atanh(x)

5) Другие:

v exp(x) экспонента

v ln(x) натуральный логарифм

v log(x) десятичный логарифм

v Re(z) вещественная часть числа z

v Im(z) мнимая часть числа z

v arg(z) аргумент комплексного числа z

v floor(x) наибольшее целое < x (x - вещест.)

v ceil(x) наименьшее целое > x (x - вещест.)

v mod(x,y) остаток от деления x на y (x,y - вещественные)

v rnd(x) случайное число из промежутка [0,x]

И.т.д.

Решение уравнений

В общем случае уравнение с одним неизвестным можно свести к виду f(x)=0. Всякое число ξ (действительное или мнимое) на отрезке [a, b] обращающее уравнение в тождество f(ξ)=0 называется корнем уравнения или его решением. Решение задачи приближенного решения уравнения состоит из двух этапов:

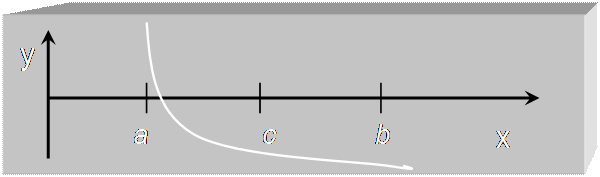
1. Отделение корнейзаключается в поиске интервалов на отрезке [a, b], которые содержат только один корень уравнения. Или отделение корней заключается в поиске значения близкого к решению. Первый этап можно выполнить по графику функции.

2. Уточнение корней заключается в непосредственном вычислении значений корней на найденных интервалах с заданной точностью ε.

Рассмотрим простейший численный метод уточнения корня уравнения. В основе метода лежит деления отрезка [a, b], на котором определен корень уравнения, пополам. Алгоритм метода следующий:

1. Для нахождения корня уравнения f(x)=0 на отрезке [a, b] делим отрезок пополам точкой с. с = (a+b)/2

2. Рассматриваются отрезки [a, с] и [с, b] и выбираем отрезок на концах которого функция f(x) имеет противоположные знаки. Если f(a)•f(с)<0 выбираем отрезок [a, с] в ином случае выбираем отрезок [с, b].

3. Для выбранного отрезка повторяем шаг 1 и шаг 2 до тех пор пока величина очередного отрезка не станет меньше заданной точности ε.

Для поиска нулей функции, а также корней уравнения применяется встроенная функция root. Формат функции:

root(выражение,имя_переменной)

Чтобы найти нуль функции (или корень уравнения):

1) задайте начальное предполагаемое значение неизвестного;

2) задайте значение точности TOL :=….;

3) используйте функцию root для решения.

Например, организовать поиск корня уравнения x3+x+1=0 можно следующим образом:

x:=0.5 TOL := 0,0001 res := root (x3+x+1,x)