Полный факторный эксперимент
В тех случаях, когда информация о функционировании объекта недостаточна или невозможно составить его детерминированную модель, прибегают к экспериментально-статистическим методам. При этом процесс рассматривают как “черный ящик”. Различают пассивный и активный эксперимент.
Активный эксперимент ставится по заранее составленному плану (планирование эксперимента). Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для получения математической модели процесса [1]. Планирование эксперимента позволяет варьировать ряд факторов и получать одновременно количественные оценки всех проявляющихся эффектов. При этом, в отличие от классического регрессионного анализа, удается избежать корреляции между коэффициентами уравнения регрессии.
В случае, когда число факторов известно, можно найти число опытов, необходимое для реализации всех возможных сочетаний уровней факторов: 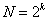 , где N – число опытов, k – число факторов, 2 – число уровней. В общем случае эксперимент, в котором реализуются всевозможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Если число уровней каждого фактора равно двум, то имеет место полный факторный эксперимент типа 2k.
, где N – число опытов, k – число факторов, 2 – число уровней. В общем случае эксперимент, в котором реализуются всевозможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Если число уровней каждого фактора равно двум, то имеет место полный факторный эксперимент типа 2k.
Нетрудно написать все сочетания уровней в эксперименте с двумя факторами. В планировании эксперимента используются кодированные значения факторов: +1 и –1 (часто для простоты записи единицы опускают). Условия эксперимента можно записать в виде таблицы, где строки соответствуют различным опытам, а столбцы – значениям факторов. Будем называть такие таблицы матрицами планирования эксперимента (табл. 1).
Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку вектор-строкой. Таким образом, мы имеем 3 вектор-столбца факторных переменных и один вектор-столбец параметра оптимизации.
Таблица 1 - Матрица планирования для трех факторов
| № опыта | x1 | x2 | x3 | y |
| – | – | + | y1 | |
| + | – | + | y2 | |
| – | + | + | y3 | |
| + | + | + | y4 | |
| – | – | – | y5 | |
| + | – | – | y6 | |
| – | + | – | y7 | |
| + | + | – | y8 |
При добавлении нового фактора каждая комбинация уровней исходного плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Отсюда появляется прием: записать исходный план для одного уровня нового фактора, а затем повторить его для другого уровня.
Эксперимент планируется для того, чтобы получить модель, обладающую некоторыми оптимальными свойствами. Оценки коэффициентов модели должны быть наилучшими и точность предсказания параметра оптимизации не должна зависеть от направления в факторном пространстве, т.к. заранее неясно, куда предстоит двигаться при поиске оптимума.
Из построения матрицы следуют два свойства:
1) первое свойство – симметричность относительно центра эксперимента – формулируется следующим образом: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю
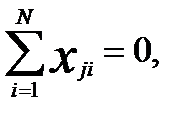
где j – номер фактора, N – число опытов, i = 1, 2, ..., k .
2) второе свойство – условие нормировки – формулируется следующим образом: сумма квадратов элементов каждого столбца равна числу опытов
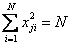
Это следствие того, что значения факторов в матрице кодируются +1 и –1.
Третье свойство - сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю
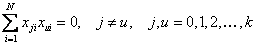 .
.
Это свойство называется ортогональностью матрицы планирования.
Четвертое свойство называется ротатабельностью, т.е. точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.
Уровни факторов в ПФЭ представляют собой границы исследуемой области (минимальное и максимальное значение фактора). Зная максимальное zi max и минимальное zi min значения факторных переменных можно определить координаты центра плана, так называемый основной уровень zi 0, а также шаг варьирования Δzi :
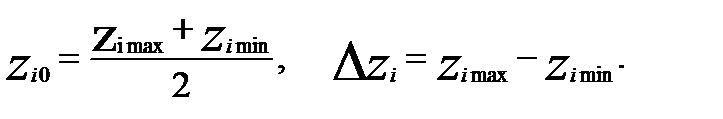 (1)
(1)
При выборе верхнего и нижнего уровней факторов необходимо учитывать ограничения, связанные со свойствами объекта исследования. На интервал варьирования так же накладываются ограничения: он не может быть меньше ошибки, с которой экспериментатор фиксирует уровень фактора, и не может быть настолько большим, что верхний и нижний уровень окажутся за пределами области определения.
От систем координат z1, z2, …zk необходимо перейти к новой безразмерной системе координат x1,x2 …, xk с помощью линейного преобразования:
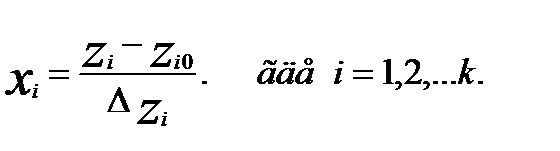 (2)
(2)
Благодаря кодированию факторов расчет коэффициентов уравнения регрессии превращаются в простую арифметическую процедуру. Коэффициенты уравнения вычисляются по формуле:
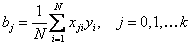 (3)
(3)
Эксперимент проводится для проверки гипотезы о том, что линейная модель
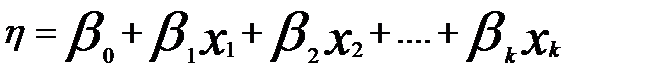
адекватна. Греческие буквы использованы для обозначения «истинных» значений неизвестных коэффициентов модели. Эксперимент позволяет только получить выборочные оценки для коэффициентов уравнения
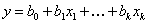 . (4)
. (4)
Их точность и надежность зависят от свойств выборки и нуждаются в статистической проверке.
Для вычисления коэффициента b0, в матрицу планирования вводят вектор-столбец фиктивной переменной x0, которая принимает во всех опытах значение +1. Это было учтено в записи формулы (3), где j принимало значения от 0 до k.
Коэффициенты при факторных переменных указывают на силу их влияния. Чем больше величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет знак плюс, то с увеличением значения фактора параметр оптимизации увеличивается, а если минус - уменьшается.
Планируя эксперимент, на первом этапе исследователь стремимся получить линейную модель. Однако нет гарантии, что в выбранных интервалах варьирования процесс описывается линейной моделью. Существуют способы проверки пригодности линейной модели (проверка адекватности).
Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор. В этом случае говорят, что имеет место эффект взаимодействия двух факторов. Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, воспользоваться правилом перемножения столбцов, получить столбец произведения двух факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия с новым вектор - столбцом, можно обращаться так же, как с вектор - столбцом любого фактора. При добавлении столбцов эффектов взаимодействий все рассмотренные свойства матриц планирования сохраняются. В этом случае модель выглядит следующим образом:
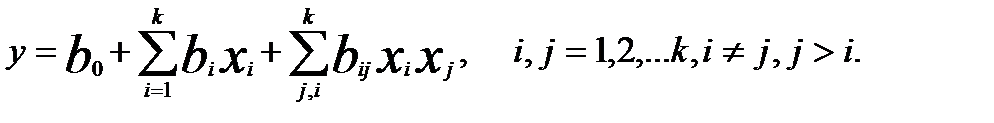 (5)
(5)
Коэффициент bij вычисляется обычным путем (3). Столбцы x1, x2,….xk задают планирование – по ним определяются условия опытов, а столбцы x0и xixj служат только для расчета соответствующих коэффициентов модели.
Необходимо обратить внимание на то, что при оптимизации стремятся сделать эффекты взаимодействия возможно меньшими. В задачах интерполяции их выявление часто важно и интересно.
Физический смысл эффекта взаимодействия можно пояснить следующим примером. Пусть на некоторый процесс влияют два фактора: температура и время реакции. В области низких температур увеличение времени увеличивает выход продукта. При переходе в область высоких температур эта закономерность нарушается. Здесь необходимо уменьшать время реакции. В этом заключается проявление эффекта взаимодействия.
Ортогональность матрицы планирования позволяет получить независимые друг от друга оценки коэффициентов модели. Величина любого коэффициента не зависит от того, какие величины имеют другие коэффициенты. Это справедливо лишь в том случае, если модель включает только линейные эффекты и эффекты взаимодействия.
Коэффициенты регрессии не коррелированны между собой. Значимость для каждого коэффициента в отдельности проверяется по критерию Стьюдента. Исключение из уравнения регрессии (5) незначимого коэффициента не сказывается на остальных коэффициентах. Все коэффициенты уравнения определяются с одинаковой точностью. Среднеквадратичная погрешность коэффициентов вычисляется по формуле:
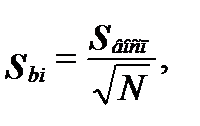 (6)
(6)
где sвосп- среднеквадратичная погрешность воспроизведения опытов, оценивается по параллельным опытам в центре плана.
Расчетное значение критерия Стьюдента определяется по формуле:
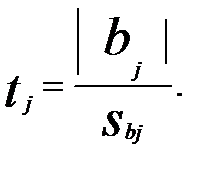 (7)
(7)
Расчетные значения критерия Стьюдента сравнивается с табличным значением для соответствующего уровня значимости. Если расчетное значение меньше табличного, то такой коэффициент исключаются из уравнения регрессии.
Незначимость коэффициентов может быть обусловлена следующими причинами:
1) основной уровень zi 0 близок к точке частного экстремума по переменной zi ;
2) малый шаг варьирования 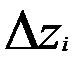 ;
;
3) переменная zi не имеет функциональной связи с зависимой переменной «y»;
4) велика ошибка воспроизводимости эксперимента.
После проверки значимости коэффициентов проверяется адекватность полученного уравнения регрессии, используя критерий Фишера:
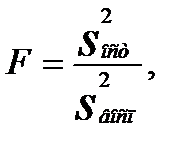 (8)
(8)
где остаточная дисперсия рассчитывается по формуле:
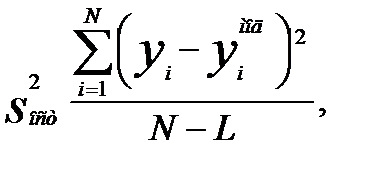 (9)
(9)
где yмод - рассчитанное по модели значение зависимой переменной (параметр оптимизации); L - число значимых коэффициентов в уравнении регрессии.
Расчетное значение критерия адекватности сравнивают с табличным значением критерия Фишера (при соответствующим уровне значимости). При этом, если расчетное значение критерия меньше табличного, то полученное уравнение регрессии адекватно описывает эксперимент.
Если гипотеза адекватности отвергается, то необходимо переходить к боле сложной форме уравнения регрессии, либо провести эксперимент с меньшим шагом 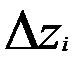 . При этом растет влияние помех, уменьшаются значения коэффициентов bi.
. При этом растет влияние помех, уменьшаются значения коэффициентов bi.
Дата добавления: 2017-09-19; просмотров: 2847;
