Лекция 2. ТОЧКА НА ЭПЮРЕ МОНЖА

2.1. Аппарат полного проецирования.

2.2. Эпюр точки.

2.3. Характеристика точек.

2.4. Контрольные вопросы.

Аппарат полного проецирования

Выше было указано, что бы обеспечить взаимно-однозначное соответ­ствие между фигурами Ф пространства и их двумерными изображениями необходимо чтобы аппарат проецирования имел несколько плоскостей проецирования.

Рассмотрим аппарат полного проецирования (метод трех изображений). Для этого введём три плоскости проекций (рис. 14):

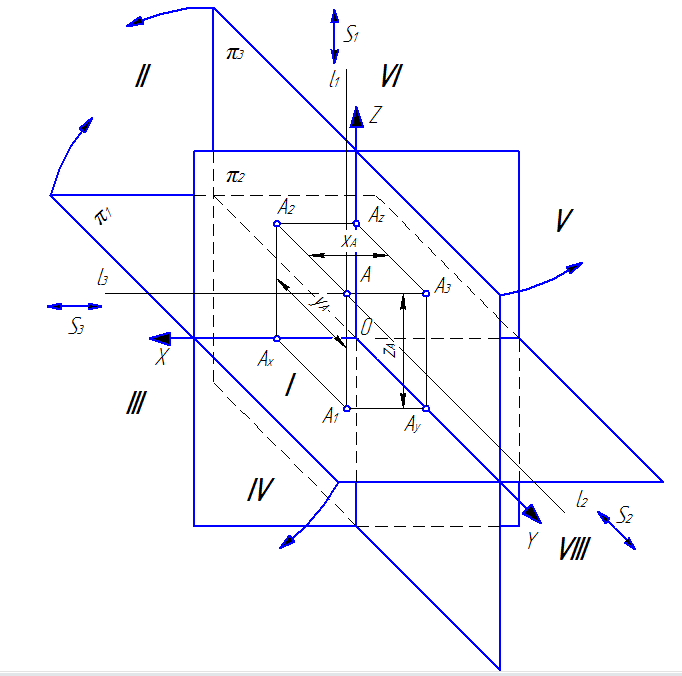
Рис. 14

π₁ – горизонтальная плоскость проекций;

π₂ – фронтальная плоскость проекций;

π₃ – профильная плоскость проекций.

Плоскости проекций располагаются взаимно перпендикулярно (π₁^π₂^ π₃), а их линии пересечения образуют оси:

– пересечение плоскостей π₁ иπ₂образуют ось 0Х (π₁ ∩π₂ = 0Х);

– пересечение плоскостей π₁ иπ₃образуют ось 0Y (π₁ ∩π₃ = 0Y);

– пересечение плоскостей π₂ иπ₃образуют ось 0Z (π₂ ∩π₃ = 0Z).

Точка пересечения осей считается точкой начала отсчета (точка 0).

Так как плоскости и оси взаимно перпендикулярны, то такой аппарат аналогичен декартовой системе координат.

Плоскости проекций все пространство делят на восемь октантов (на рис. 14 они обозначены римскими цифрами). Плоскости проекций считаются непрозрачными, а зритель всегда находится в I октанте.

Проецирование ортогональное с центрами проецирования S₁, S₂ и S₃ соответственно для горизонтальной, фронтальной и профильной плоско­стей проекций.

Рассмотрим работу аппарата на примере проецирования точки А.

Из центров проецирования S₁, S₂ и S₃ выходят проецирующие лучи l₁, l₂ и l₃. Эти лучи проходят через точку А и пересекаясь с плоскостями проекций образуют ее проекции:

– А₁ – горизонтальная проекция точки А;

– А₂ – фронтальная проекция точки А;

– А₃ – профильная проекция точки А.

Точка в пространстве характеризуется своими координатами A(x,y,z). Точки A_x, A_y и A_z соответственно на осях 0X, 0Y и 0Z показывают координаты x, y и z точки А. На рис. 14 даны все необходимые обозначения и показаны связи между точкой А пространства, её проекциями и координатами.

Эпюр точки

Чтобы получить чертёж точки А (рис. 15), в аппарате проецирования (рис. 14) плоскость π₁ с полученной проекцией точки А₁ вращают по часовой стрелке вокруг оси 0Х, до совмещения её с плоскостью π₂. Затем плоскость π₃ с проекцией точки А₃, вращают против часовой стрелки вокруг оси 0Z, до совмещения её с плоскостью π₂. Направление поворотов плоскостей π₂ и π₃ показано на рис. 13 стрелками. Полученный таким образом чертёж называется эпюром. При этом прямые А₁А_х и А₂А_х станут располагаться на общем к оси 0Х перпендикуляре А₁А₂, а прямые А₂А_х и А₃А_х станут располагаться на общем к оси 0Z перпендикуляре А₂А₃. Эти прямые в даль­нейшем будем называть соответственно вертикальной и горизонтальной линиями связей.

Следует отметить, что при переходе от аппарата проецирования к эпюру проектируемый объект исчезает, но вся информация о его форме, геометрических размерах и месте его положения в пространстве сохраняются.

На практике построение эпюра точки А(x_A, y_A, z_A) осуществляется по числен­ным значениям ее координат x_A, y_A и z_A в следующей последо­вательности (рис. 15). Эта последовательность называется методикой построения эпюра точки.

1. Ортогонально вычерчиваются оси OX, OY и OZ.

2. На оси OX откладывается численное значение координаты x_A точки А и получают положение точки А_х.

3. Через точку А_х перпендикулярно оси OX проводится вертикальная линия связи.

4. На вертикальной линии связи от точки А_х по направлению оси OY откладывается численное значение координаты y_A точки А и определяется положение горизонтальной проекции точки А₁ на эпюре.

5. На вертикальной линии связи от точки А_х по направлению оси OZ откладывается численное значение координаты z_A точки А и определяется положение фронтальной проекции точки А₂ на эпюре.

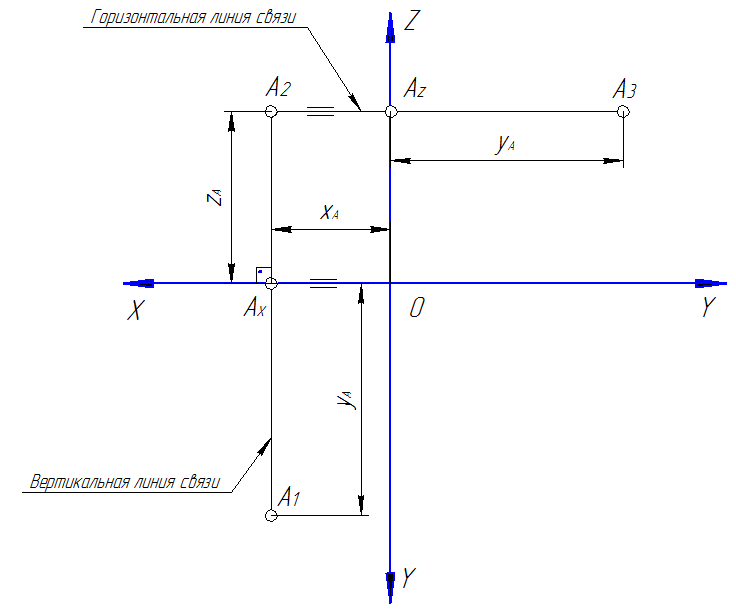
Рис. 15

6. Через точку А₂ параллельно оси OX проводится горизонтальная линия связи. Пересечение этой линии и оси OZ даст положение точки А_z.

7. На горизонтальной линии связи от точки А_z по направлению оси OY откладывается численное значение координаты y_A точки А и определяется положение профильной проекции точки А₃ на эпюре.