Сравнение методов чистого приведенного значения и внутренней доходности

Во многих отношениях метод чистого приведенного значения лучше метода внутренней доходности, и поэтому можно объяснить только метод NPV, утверждая, что IRR менее удобен. Однако метод внутренней доходности также хорошо знаком многим корпоративным руководителям, он широко популярен в практическом бизнесе и имеет ряд достоинств. Следовательно, важно, чтобы вы понимали и его, а также могли объяснить, почему иногда проект с более низкой IRR на самом деле оказывается предпочтительнее альтернативного проекта с более высокой внутренней доходностью.

Профили чистого приведенного значения.График, на котором изображается чистое приведенное значение проекта в зависимости от его стоимость капитала, называется профилем чистого приведенного значения (NPV); профили проектов L и S приведены на рис. 5.5. При нулевой стоимости капитала чистое приведенное значение просто равно общей сумме недисконтированных потоков денежных средств проекта.

Следует вспомнить, что внутренняя доходность определяется как учетная ставка, при которой чистое приведенное значение проекта равно нулю. Следовательно, точка, в которой профиль ее чистого приведенного значения пересекает горизонтальную ось, указывает внутреннюю доходность проекта. Поскольку мы вычислили IRR_S и IRR_L в предыдущем разделе, мы можем подтвердить этот вывод.

Профили чистого приведенного значения могут оказаться весьма полезными при анализе проектов, и мы будем часто использовать их в оставшейся части главы.

На рис. 5.5 показано, что профили чистого приведенного значения как проекта L, так и проекта S снижаются по мере увеличения стоимости капитала. Проект L имеет более высокое значение NPV при низкой стоимости капитала, в то время как S имеет более высокое чистое приведенное значение, если стоимость капитала выше ставки перелома, равной 7,2%. Заметьте также, что NPV проекта L более чувствительно к изменениям стоимости капитала, чем проекта S: одинаковое изменение к оказывает большое влияние на NPV _L, чем на NPV _S. Это происходит оттого, что проект S является краткосрочным, а L – долгосрочным, а рост стоимости капитала оказывает значительно большее влияние на отдаленные, чем на ближайшие потоки денежных средств. Таким образом, если проект обеспечивает большую часть денежных потоков в ближайшие годы, его чистое приведенное значение будет снижаться с ростом стоимости капитала не слишком резко, NPV же проекта, потоки денежных средств которого поступают позднее, из-за роста стоимости капитала может пострадать более серьезно.

Рис. 5.5. Профили чистого приведенного значения: NPV проектов L и S при различных значениях стоимости капитала

Взаимоисключающие проекты.Теперь давайте предположим, что проекты L и S являются взаимоисключающими, а не независимыми. Иначе говоря, мы можем выбрать либо проект S, либо проект L, либо отклонить оба проекта, но мы не можем принять оба.

На рис. 5.5 видно, что, если стоимость капитала к больше ставки перелома, равной 7,2%, оба метода NPV и IRR приводят к выбору проекта S. однако если стоимость капитала меньше ставки перелома, то по методу чистого приведенного значения проекта L оценивается выше, в то время как метод внутренней доходности подсказывает, что проект S предпочтительней. Таким образом, если стоимость капитала меньше ставки перелома, то выводы этих двух критериев противоречат друг другу. Метод чистого приведенного значения подсказывает выбор проекта L, тогда как методу внутренней доходности выбирает S. Какой же выбор в таком случае считать верным? Логика подсказывает, что метод чистого приведенного значения лучше, поскольку он позволяет выбрать проект, максимально увеличивающий благосостояние акционеров.

Профили чистого приведенного значения проектов чаще всего пересекаются, и это приводит к возникновению противоречий в следующих двух случаях: 1) когда существует значительные различия в масштабах проектов, что означает, что затраты на осуществление одного из них существенно превосходят затраты на осуществление другого; и 2) когда распределение потоков денежных средств по времени от двух проектов отличается настолько существенно, что большая часть потоков денежных средств от одного проекта поступает в первые годы, в то время как от другого проекта – позднее. Именно этот случай и демонстрирует наш пример с проектами S и L.

Ключ к разрешению конфликтов между взаимоисключающими проектами содержится в ответе на следующий вопрос: насколько полезнее генерировать потоки денежных средств раньше, чем позже? Предпочтение раннего получения денежных потоков зависит от дохода, который мы можем получить по ним позднее, т.е. ставки, при которой мы можем их реинвестировать. При этом метод чистого приведенного значения предполагает, что ставка, по которой потоки денежных средств могут быть реинвестированы, - это стоимость капитала проекта, в то время как использование метода внутренней доходности подразумевает, что фирма может реинвестировать средства по этой ставке IRR.

Какое из предложений более естественно: что потоки денежных средств могут быть реинвестированы по стоимости капитала или по ставке внутренней рентабельности проекта? Очевидно, предложение о реинвестировании денежных потоков проекта по его стоимости капитала более реалистично, поскольку эта стоимость определяется затратами на обслуживание капитала, привлеченного извне проекта. Следовательно, мы приходим к заключению о том, что метод NPV более обоснован: он опирается на более разумное предположение о реинвестировании по стоимости капитала.

В заключение еще раз повторим, что в случае, когда проекты являются независимыми, и метод чистого приведенного значения, и метод внутренней доходности приводят к совершенно одинаковому решению о принятии или отклонении данного проекта. Однако при оценке взаимоисключающих проектов, особенно проектов, отличающих своими масштабами или распределением денежных потоков по времени, должен применяться метод чистого приведенного значения.

Множественные внутренние доходности.Существует еще одна ситуация, в которой нельзя применить метод внутренней доходности, - это случай, когда рассматриваются проекты с необычными потоками денежных средств. Считается, что проект имеет обычные денежные потоки, если он вначале предполагает наличие одного или нескольких исходящих потоков (затрат), за которыми следует ряд входящих потоков (денежных поступлений). Однако если проект требует исходящего потока денежных средств в некоторый момент по ходу его реализации, то проект считается необычным. Проекты с необычными потоками денежных средств представляют особую сложность, когда они оцениваются по методу внутренней доходности, и наиболее часто возникающая в этом случае проблема – это проблема множественности IRR.

Оказывается, что если решить уравнение (5.2) относительно внутренней доходности проекта с необычными потоками денежных средств, то можно получить более одного значения IRR.

На самом деле уравнение (5.2) представляет собой многочлен степени n, и поэтому оно в принципе имеет n различных корней (решений). Если денежные потоки по проекту обычные, то все корни этого многочлена, кроме одного, - комплексные либо отрицательные, что, очевидно, бессмысленно, и поэтому получается только одно значение IRR. Однако когда проект имеет необычные потоки денежных средств, возникает возможность появления нескольких положительных вещественных корней.

Чтобы проиллюстрировать это, предположим, что фирма рассматривает возможность затратить 1,6 млн. ден.ед. на разработку открытого угольного разреза (проект М). Проект принесет поток денежных средств в размере 10 млн. ден.ед. в конце года 1, но позднее, в конце года 2, те же 10 млн. ден.ед. будут потрачены на рекультивацию территории. Следовательно, предполагаемые чистые потоки денежных средств проекта будут таковы (в млн. ден.ед.):

Соответственно уравнение (5.2) в данном случае будет иметь следующий вид:

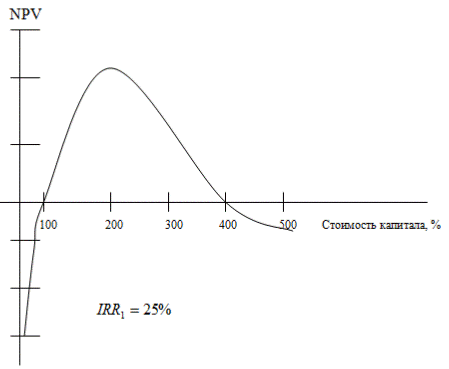
Рис. 5.6. Внутренняя доходность проекта М

Несмотря на то что практически все теоретические работы однозначно указывают на то, что в случае противоречивости выводов критериев NPV и IRR следует использовать метод чистого приведенного значения, опросы показывают, что многие руководители, тем не менее, отдают предпочтение скорее методу внутренней доходности. Очевидно, менеджеры интуитивно считают его более привлекательным для оценки вложений в наглядных терминах дисконтированных денежных потоков.

Можно ли мы, учитывая этот факт, придумать показатель процентной оценки, который был бы свободен от недостатков внутренней доходности? Ответ оказывается довольно часто положительным. Показатель, на котором основан новый критерий, называется модифицированный внутренней доходностью (IRR, MIRR). Он определяется следующим образом:

где PV - будущая стоимость денежных поступлений (FV), (5.3)
COF обозначает исходящие потоки денежных средств, а CIF - входящие потоки. Таким образом, член уравнения, стоящий слева, - это просто приведенное значение затрат при дисконтировании при стоимости капитала, а числитель правого члена уравнения – это наращенное, будущее значение FV входящих потоков. Ставка дисконтирования, приравнивающая приведенное значение FV приведенному значению затрат, как раз и называется модифицированной внутренней доходностью (MIRR).

Если компания несет затраты в момент времени t=0 и если первый входящий поток денежных средств от операций происходит во время t=1, как в случае проектов S и L, представленных на рис.12.1, то можно использовать также и формулы (12.4):

Затраты = CОF 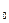= 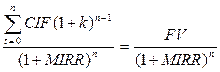(5.4)

Мы можем проиллюстрировать это уравнение на примере проекта S (рис. 5.7):

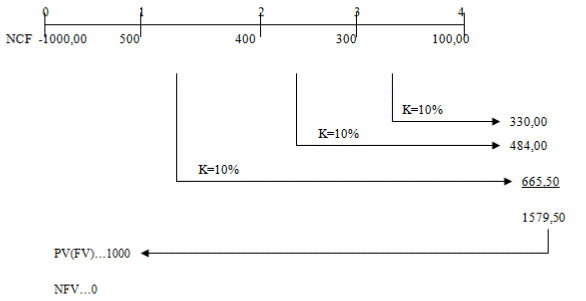
Рис. 5.7 Практическая иллюстрация уравнения (5.4)

В итоге мы получаем MIRR =12,1%. Аналогично мы находим MIRR 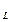=11,3%. Модифицированная внутренняя доходность MIRR имеет значительное преимущество перед обычной внутренней рентабельностью IRR. Так, расчет MIRR подразумевает, что потоки денежных средств от всех проектов реинвестируются пот стоимости капитала, в то время как обычная внутренняя доходность подразумевает, что потоки денежных средств от каждого проекта реинвестируются по собственной внутренней ставке проекта. Поскольку реинвестирование по стоимости капитала в общем случае более корректно, MIRR – лучший показатель действительной рентабельности проекта. Кроме того, модифицированная внутренняя доходность также решает проблему множественности ставок IRR.

Возникает вопрос: одинаково ли приемлемы на практике методы модифицированной внутренней доходности и чистого приведенного значения для выбора из двух взаимоисключающих проектов? Если два проекта имеют одинаковый масштаб и одинаковый срок жизни, то анализ по методам чистого приведенного значения и MIRR всегда приводит к одному и тому же решению. Кроме того, если проекты имеют одинаковый масштаб, но различные сроки жизни, то метод модифицированной внутренней доходности всегда приводит к тому же решению, что и метод чистого приведенного значения, если для обоих проектов MIRR рассчитывается в предположении, что срок их жизни равен сроку более долгосрочного проекта (для более «короткого» проекта недостающие денежные потоки считаются нулевыми). Однако если проекты имеют различные масштабы, противоречия между выводами этих критериев все равно могут возникать. Например, если бы мы выбрали между крупными проектами L и небольшим проектам S, которые были бы взаимоисключающими, мы могли бы столкнуться с ситуацией, когда 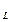NPV > NPV , но MIRR > MIRR .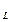

В итоге мы приходим к заключению о том, что модифицированная внутренняя доходность предпочтительна по отношению к «обычной» внутренней доходности в качестве показателя «действительной» нормы прибыли проекта, но метод чистого приведенного значения все равно остается лучшим способом выбора между конкурирующими проектами, поскольку он обеспечивает более точную демонстрацию того, что каждый проект увеличит стоимость фирмы.