Коэффициентов уравнения регрессии

Построенная методом наименьших квадратов модель представляет лишь оценки коэффициентов регрессии. Поэтому важно проверить, насколько представительны данные оценки относительно истинных параметров модели. Это достигается проверкой статистической надежности (значимости) коэффициентов регрессии и близости расположения фактических данных к рассчитанной линии регрессии.

Проверка статистической значимости состоит в следующем. Выдвигается нулевая гипотеза Н₀ о том, что коэффициенты статистически незначимо отличаются от нуля, и альтернативная ей гипотеза Н₁:

Н₀: b₀ = 0, Н₁: b₀ ¹ 0,

Н₀: b₁ = 0, Н₁: b₁ ¹ 0,

. . . . . . . . . . . . . . . . . . . . . . . . . . . .

Н₀: b_р = 0, Н₁: b_р ¹ 0

Для проверки этих гипотез используются t-критерии, которые рассчитываются делением оценок на их стандартные ошибки

.

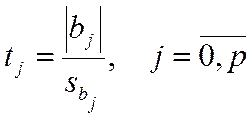Стандартные ошибки коэффициентов – это корни квадратные их дисперсий:

для парной модели

, ,

;

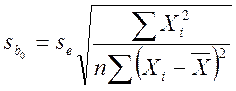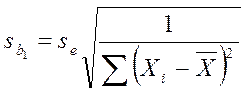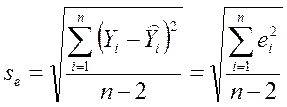для многофакторной модели:

,

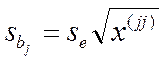где 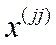– диагональные элементы матрицы ,

.

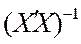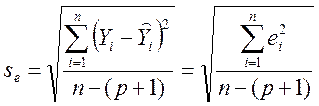t-критерии для каждой независимой переменной истолковываются так же, как и раньше, но в случае многофакторной модели они имеют t-распределение с n – (р + 1) степенями свободы (если в модели р независимых переменных, то будет (р + 1) коэффициентов регрессии, включая свободный член).

Обычно статистическую значимость проверяют при уровне доверительной вероятности 95% или 99%. Это означает, что существует вероятность 95% или 99%, что значения b0 и b1 не случайны и являются значимыми оценками соответствующих параметров. Коэффициенты регрессии значимы, если t-критерий больше величины, указанной в таблице t-распределения.

В случае с фондовыми индексами имеем: b₁ = 5,9640, ,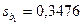

b₀ = 196,3298, . Следовательно, t-критерий равен:

, .

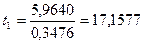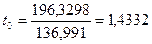Нам необходимо решить, будет ли проверка значимости «односторонней» или «двусторонней», причем решить это надо еще до того, как станут известны результаты регрессии. Выбор определяется теоретическим обоснованием модели связи Х и Y, проверяемой с помощью регрессии.

При односторонней проверке проверяется значимость коэффициентов регрессии, когда ожидаемая взаимосвязь между Х и Y может быть или положительной (прямой), или отрицательной (обратной), но не той и другой одновременно.