Двусторонняя проверка проверяет значимость, когда взаимосвязь между Х иY может быть и положительной, и отрицательной.

Для проверки статистической надежности можно использовать интервальное оценивание коэффициентов регрессии.

Для значений параметров модели b_j, j = 0,1,2,…,p строятся доверительные интервалы, которые будут приемлемы с вероятностью (1 – a) при найденных оценках b_j:

,

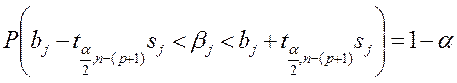где 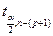– табличное значение статистики Стьюдента при выбранном

уровне значимости и n – (p + 1) степенях свободы;

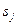–стандартная ошибка оценки, равная: .

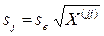Вывод о статистической надежности оценки делают исходя из знаков границ доверительного интервала: если эти знаки одинаковы, то нулевая гипотеза о равенстве истинного значения параметра нулю отклоняется в пользу альтернативной гипотезы при вероятности (1 –a); в противном случае нулевая гипотеза не отклоняется, и соответствующий коэффициент b_j считается статистически не значимой характеристикой параметра.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 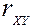. Существуют различные формулы для его определения:

.

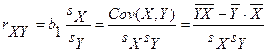Как известно, линейный коэффициент корреляции находится в границах:

-1 £ 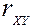£ 1.

Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между переменными может оказаться достаточно тесной.