Деятельности оператора: модели оператора
Математические модели, построенные на основе структурного подхода, обладают существенным недостатком, заключающемся в представлении структуры деятельности оператора в неизменяющемся, постоянном виде. (Сказанное не относится только к моделям, в основе которых лежат функциональные сети). Для преодоления этого недостатка Г.В. Суходольским предложены понятия вероятностного алгоритма и случайной структуры, которые реализуются им при построении структурно-алгоритмических моделей деятельности [111,178]. Эта модель использует математический аппарат теории графов и матричной алгебры и представляется в виде абстрактного графа деятельности (равновесного стохастического мультиграфа).
Абстрактный граф деятельности (АГД) представляет собой некоторую конечную совокупность вершин отображающих элементы деятельности (людей, предметы и орудия труда, реализуемые операции), и сопоставленную этим вершинам совокупность дуг, характеризующих связи между элементами деятельности (материальные, информационные, энергетические). АГД можно рассматривать как наиболее общую модель деятельности, поскольку в принципе его дугам и вершинам могут быть приписаны любые качественные и количественные характеристики. При этом дуги АГД могут быть определены любым математическим и физическим образом. Благодаря этому, а также специально разработанному новому математическому аппарату построения вероятностных алгоритмов и синтеза равновесных мультиграфов оказывается возможным математически описывать практически любую сложную деятельность, а далее на полученном описании использовать другие известные модели деятельности.
Так, рассмотренные выше сервомодели (модели слежения), основанные на использовании передаточных функций, могут быть представлены как ориентированные или неориентированные графы, вершины которых есть условно выделяемые звенья (усилительные, инерционные, дифференцирующие, интегрирующие и т. п.) с известными передаточными свойствами, а дуги (ребра) имеют смысл входных и выходных переменных. Информационные модели представляют собой подграфы от стохастического орграфа, вершины которого есть вероятностно характеризуемые признаки, определенные на множестве средств индикации, а также состояния системы, определяемые этими признаками, а дуги — импликации. Точно также можно показать, что и другие модели деятельности в конечном итоге могут быть сведены к АГД.
Такому графу и его модификациям однозначно соответствует ряд матриц: матрица смежности; матрица, описывающая вероятностный алгоритм решения каждой задачи в любом из режимов работы; матрица для каждого режима работы; матрица для описания работы оператора во всех режимах. Исходной является матрица смежности, остальные получаются на ее основе с помощью специально введенной операции обобщения. Полученные в матричной форме выражения позволяют получить математические модели на разных структурно-алгоритмических уровнях: реализации алгоритма, алгоритма задачи, индивидуальной задачи, коллективной задачи. Каждая из этих моделей может быть построена в двух специфических формах: операционно-логической и предметно-функциональной.
В первом случае модель представляется в виде графа, вершинами которого являются коды сенсорных, моторных и логических операций, а дугами — импликации, характеризуемые частотой. Во втором случае модель также представляется в виде графа. Однако вершины в нем определены предметно, в виде средств контроля и управления, а дуги, характеризуемые частотой, определены функционально как пространственные перемещения специалиста, а также в виде поступающей к нему и исходящей от него информации. Большое внимание при построении моделей уделяется вопросу получения оценок для взвешивания частотных алгоритмов и способам синтеза более крупных структур из подструктур, оптимальных на уровне частных алгоритмов.
В разработанных моделях используются: перечисление реализаций частных алгоритмов при наиболее вероятных сочетаниях логических условий; специальное матричное представление этих реализаций и их объединение в виде
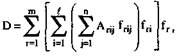 (8.4)
(8.4)
где D — надматрица, отображающая модель деятельности для 1 задач, m режимов работы и п способов решения каждой задачи; АГц — подматрица j-й реализации i-ro частотного алгоритма в r-ом режиме (j=l,n; i= 1Д;г= l,m); 1щ, Ir;, Ir — частота j-ro способа i-й задачи и r-го режима работы соответственно.
Путем введения специальной оценки эффективности труда оператора данная модель позволяет осуществить оптимальную компоновку рабочего места оператора.
Помимо использования для построения структурно-алгоритмических моделей деятельности оператора теория графов используется в инженерной психологии и для решения целого ряда других задач: для оптимального размещения людей и машин в рабочих помещениях и оборудования на рабочем месте [111,178];
для описания и анализа потоков информации в системах контроля и управления [135, 178]; для описания и машинного моделирования процессов памяти, оперативного мышления и принятия решений [151, 100]; для описания и анализа организационной структуры трудового коллектива — формальной и неформальной [25, 175]. Методы теории графов лежат также в основе одного из подходов к построению семантической теории информации [70].
Для построения моделей оператора может использоваться и математический аппарат теории игр; такие модели называются игровыми. Теорией игр называется раздел математики, изучающий абстрактные модели конфликтных ситуаций. Под конфликтной понимается ситуация (игра), в которой участвуют как минимум два игрока (лица, коллективы, управляющие системы), стремящиеся по некоторым определенным в игре правилам обеспечить себе максимальный выигрыш. Интересы игроков полностью или частично противоположны, то есть всякое улучшение положения одного игрока ухудшает положение другого. Простейшей схемой теории игр является конечная игра двух лиц с нулевой суммой. При этом каждый игрок независимо от другого выбирает одну из конечного числа возможностей. Каждой паре выбранных возможностей соответствует некоторый выигрыш одного игрока, равный проигрышу другого, то есть сумма выигрышей обоих игроков равна нулю. Цель теории игр заключается в выработке рекомендаций для определения оптимальной стратегии каждого из участников игры. Все рекомендации выбираются в предположении, что противник является разумным и делает все для того, чтобы помешать игроку добиться своей цели. Поэтому возможности применения теории игр для создания моделей деятельности оператора весьма ограничены, поскольку он, как правило имеет дело с неразумным «противником». В этом плане весьма спорным является утверждение о том, что одним из наиболее перспективных направлений развития моделирования для проектирования деятельности человека является использование математического аппарата теории игр [55]. К сожалению, реальное положение дел не соответствует этому утверждению.
Одна из самых первых и наиболее удачных игровых моделей в инженерной психологии была предложена В.Ф. Вендой для описания процесса технической диагностики (поиска отказов) человеком-оператором [17]. Модель базируется на следующих исходных условиях. Оператор получает сигнал об отклонении режима от нормы. Существует п параметров, проверка значений которых позволяет установить причину отклонения и компенсировать его одним из имеющихся способов. Чем быстрее оператор найдет причину, тем быстрее он ликвидирует отклонение; при каждой неудачной попытке — вызове «пустого» параметра или неудачном опережающем действии — оператор «платит» потерей времени и, возможно, дальнейшим ухудшением состояния объекта. Выигрыш и потеря могут быть в каждом случае оценены количественно.
Для нахождения оптимальной стратегии оператора необходимо найти оптимальную перестановочную матрицу; ее размер 2пхп2. Число последовательных шагов для получения достаточно хорошего приближения равно nm, где m — небольшое положительное число, такое что nm<n!. Процедура технической диагностики сводится к одномерному варианту игры и состоит в следующем: 1 — оператор (игрок 1) пытается определить какой из п параметров определяет наличие неисправности; 2 — параметр (игрок 2) скрыт в одном из п сигнальных элементов устройства отображения.
Игра продолжается до нахождения параметра (игрока 2), обозначенного как выигрыш оператора (игрока 1). Эту процедуру можно представить как поиск набора положительных чисел dj (чем длиннее перебор параметров, тем меньше выигрыш оператора, если же оператор не успевает предотвратить аварию и она происходит, это рассматривается как выигрыш игрока 2). Если параметр скрыт в i-м сигнальном элементе с вероятностью х,, то оператор стремиться выбрать такое i, при котором а;х; = тах (а;Х;), где а; — есть какая-либо оценка эффективности i-ro действия оператора.
Математический аппарат теории игр предлагается также использовать в качестве основного средства для описания и разрешения различного рода конфликтов в системе «человек-машина» [131]. Здесь приведена
классификация возможных конфликтов, дается их подробное математическое описание, показаны в общем виде пути их разрешения. Одним из основных путей предлагается использовать возможность преобразования неорганизованного конфликта в организованный. Рассмотрение этого вопроса ведется с позиций развиваемого автором данной работы организмического подхода к проектированию и построению СЧМ. К сожалению, предлагаемые игровые модели носят очень общий и абстрактный характер, а пути их практической реализации и примеры практического применения никоим образом не приводятся.
Наиболее широкое применение в настоящее время для описания деятельности оператора находят методы теории информации, теории массового обслуживания, теории автоматического управления. Получаемые на основе использования этих методов модели деятельности называются соответственно информационными, сервисными (или моделями обслуживания), моделями слежения. Рассмотрим их более подробно.
Применение теории информации для моделирования деятельности оператора основано на представлении его в качестве канала связи, задачей которого является передача информации со средств отображения на органы управления. Построение модели основано на расчете количества информации по формулам (2.2) и (2.3). Они представляют собой наиболее общие формулы для расчета количества информации.
Однако оператор в своей деятельности выполняет различные действия (поиск сигнала, считывание показаний с прибора, производство вычислений, управляющие движения т.п.). Для каждого из этих действий в зависимости от конкретных условий их выполнения могут быть получены частные формулы для определения количества информации.
Для получения частных формул необходимо воспользоваться двумя основными правилами.
1. Количество информации характеризует сложность выбора одного состояния из п возможных. Поэтому в любом частном случае нахождения количества информации прежде всего необходимо определить общее число возможных состояний данной
системы и их вероятности, а затем применить формулу (2.2) при неравновероятных или (2.3) при равновероятных состояниях системы. 2. К величине информации применимо правило аддитивности. Это означает, что общее количество информации, поступающей от нескольких источников, равно суммарному количеству информации от каждого источника в отдельности. Правило справедливо, если все источники взаимонезависимы. Применительно к деятельности оператора это означает, что для определения общего количества информации, перерабатываемой человеком, необходимо вначале определить количество информации, используемой при выполнении каждого действия, а затем найденные значения просуммировать.
Порядок применения этих правил рассмотрим на частном примере. На рис. 8.5 показана лицевая сторона измерительного прибора, имеющего три диапазона измерений: 50 В, 100 В и 500 В. Определим количество информации, которую перерабатывает оператор, проводя измерение на каждом из диапазонов.
На первом диапазоне оператор снимает отсчет с прибора и найденное значение делит на два. Если погрешность снятия показаний равна ±δ, то общее число различимых оператором состояний прибора равно
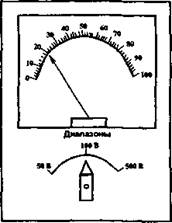
Рис. 8.5. Лицевая панель измерительного прибора.
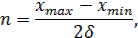
где xmax и xmin — соответственно максимальное и минимальное значение шкалы прибора.
Считая, что величина 5 равна половине цены деления шкалы и что все показания равновероятны, из формулы (2.3) следует
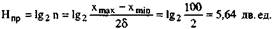
Найденное показание оператор должен разделить на два. Количество информации, используемой при вычислении, находится по формуле
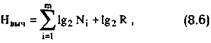
где N1 — максимально возможные значения используемых при вычислении чисел; m — количество чисел, используемых при вычислении; R — максимально возможное значение результата вычисления.
Нетрудно заметить, что формула (8.6) получена на основании приведенных выше правил. Ее применение основано на том, что при производстве вычислений человек m раз производит выбор нужного числа из N; возможных, а при получении результата — выбор одного числа из R возможных.
Подставляя исходные данные в формулу (8.6), получим: 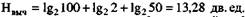
Общее количество перерабатываемой информации равно 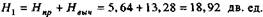
Рассмотренная стратегия поведения характерна для оператора малообученного или оператора, который сравнительно редко производит измерения на данном диапазоне. Если же оператор часто работает с прибором, то у него могут быть сформированы и храниться в памяти эталоны истинных значений для каждого значения шкалы прибора. Тогда действие по переводу отсчета со шкалы в истинное значение практически будет отсутствовать, выполняться автоматически на уровне навыка, внимание оператора на его выполнение специально не будет направлено. При каждом отсчете оператор будет извлекать из памяти хранящиеся там эталоны истинных значений измеряемого показателя и использовать их для получения конечного результата без производства специальных вычислений. Очевидно, количество перерабатываемой человеком информации будет определяться только той величиной, которую оператор получает производя отсчет по шкале прибора, т. е. в этом случае Hi=5,64 дв. ед.
Как видим, информационные методы не всегда дают однозначный ответ о результатах деятельности оператора. Даже решая одну и ту же задачу, человек может применять различные стратегии поведения. Это существенно влияет на количество информации, перерабатываемой при решении задачи.
При работе на втором диапазоне оператор сразу получает истинное значение измеряемого показателя, т. е. Н2=5,64 дв. ед. При работе на третьем диапазоне оператор помимо снятия отсчета должен умножить полученное значение на пять. Расчет количества информации производится аналогично тому, как это делалось для первого диапазона.
Методы теории информации применяются в инженерной психологии при решении ряда задач. Во-первых, количество перерабатываемой информации может использоваться как мера сложности работы оператора, следовательно, такой способ позволяет сравнивать между собой различные виды операторской деятельности. Во-вторых, зная количество информации, можно оценить время, которое затрачивает оператор на переработку этой информации, поскольку между ними, как правило, существует линейная зависимость. В-третьих, знание количества информации позволяет согласовать скорость ее выдачи (производительность источника информации) с психофизиологическими возможностями человека по ее приему и обработке. Условием неискаженной передачи информации является: Vnoc < Von, где Vnoc — скорость поступления информации к оператору; Von — пропускная способность оператора.
Величина Von зависит от характера деятельности оператора. Если он может быть представлен как канал без памяти, то величина пропускной способности лежит в пределах 10 — 70 дв.ед/с. В этом случае человек работает как простой канал передачи информации, последовательные сигналы независимы друг от друга,
предыдущий сигнал не влияет на прием следующего (печатание на машинке, корректорская работа, выполнение арифметических операций и т. п.).
Если в процессе деятельности оператору необходимо запомнить отрезок входной последовательности сигналов, не превышающий объем кратковременной памяти, то в этом случае человека можно рассматривать как канал переработки информации с кратковременной памятью. Пропускная способность имеет в этом случае порядок нескольких дв. ед. в секунду (примерно 2 — 4 дв. ед/с). Такой режим является наиболее характерным для деятельности оператора.
Если же отрезок входной информации превышает объем кратковременной памяти, то для его запоминания необходимо многократное повторение. Пропускная способность вследствие этого падает до десятых долей дв. ед. в секунду и ниже [111].
Применение теории информации для анализа деятельности оператора связано с целым рядом трудностей. Это обусловлено тем, что теория информации была создана для решения ряда задач в технике связи. Поэтому простой перенос ее методов в другую область — исследование человеческой деятельности — не всегда дает желаемые результаты.
Основные причины трудностей применения теории информации для изучения деятельности оператора заключаются в следующем:
1.В основе расчета количества информации по формулам (2.2) и (2.3) лежит длина физического алфавита сигналов и вероятностей их появления. Человек же зачастую пользуется собственным (внутренним) алфавитом сигналов, отличным от физического, а субъективные вероятности сигналов для человека не всегда совпадают с объективными. Однако принципы формирования субъективного алфавита еще до конца не раскрыты. Поэтому приходится пользоваться некоторой идеализированной моделью деятельности человека, в основу которой положены характеристики входных, а не «внутренних» сигналов человека.
2.Теория информации занимается лишь стационарными процессами, статистические характеристики которых с течением времени не меняются. Характеристики же человека ввиду его обучаемости, утомляемости, действия различных факторов беспрерывно меняются во времени.
3.Теория информации не учитывает смысловую сторону информации, ее ценность и значимость. На деятельность же оператора оказывают влияние не только статистические характеристики сигналов, но и их смысл и значение для оператора.
4.Теория информации не учитывает временную неопределенность сигналов. Для человека же имеет большое значение не только то, какие сигналы и с какой вероятностью к нему поступают, но и время их поступления [155]. Это является источником дополнительной неопределенности, которая при анализе деятельности, как правило, не учитывается.
Наличие этих трудностей накладывает существенные ограничения на применение теории информации в инженерной психологии. Игнорирование их приводит к значительному разбросу экспериментальных данных и затрудняет сопоставление результатов, полученных в разных исследованиях. Однако это не должно являться причиной отказа вообще от применения информационных методов в инженерной психологии. Как и любой другой, информационный метод справедлив лишь при определенных условиях и для решения определенных задач. Эти условия в общем виде сводятся к следующему:
■ четко определен алфавит используемых человеком сигналов и вероятности их появления;
■ сигналы по своему смысловому значению примерно равноценны для оператора;
■ характеристики работоспособности оператора в пределах изучаемого отрезка времени не претерпевают существенных изменений;
■ стратегия поведения оператора известна и не меняется в процессе решения однотипных задач;
■ число поступающих к оператору различных сигналов невелико, сами сигналы слабо зависят друг от друга;
■ временная неопределенность сигналов существенно меньше смысловой неопределенности или же она может быть учтена при расчетах количества информации.
В тех случаях, когда эти условия соблюдены, применение теории информации для изучения и описания деятельности оператора дает весьма полезные результаты [122, 168, 207]. Наряду с этим делаются интенсивные попытки совершенствования информационных методов применительно к анализу и описанию деятельности оператора. Эти попытки идут как по пути совершенствования существующих методов, использующих энтропийные оценки количества информации, так и по пути учета семантической стороны информации.
Например, в работе [155] существенно расширяется понятие энтропии по сравнению с рассмотренными выше случаями. При этом считается, что любой сигнал индикатора как источника информации может полезно служить задачам контроля и управления лишь в том случае, если он будет соотнесен ко времени его появления и экспозиции. Таким образом, для деятельности оператора важна не только статистическая (частота появления), но и временная (время появления) неопределенность. В силу этого возникает необходимость явного введения времени в исходные соотношения для оценки энтропии и количества информации. С математической точки зрения этот шаг эквивалентен переходу от уровня случайных событий на уровень случайных процессов в моделировании взаимодействия человека и машины.
При таком подходе в качестве основы для формирования выражений энтропии и количества информации необходимо рассматривать вероятности наступления тех или иных событий х; в интересующий нас момент tj на отрезке времени наблюдения 0 < t < Т, т. е. вероятности Р (х;, t). Тогда для полной количественной характеристики неопределенности ситуации с учетом неопределенности, вносимой фактором времени, будем иметь
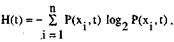 (8.7)
(8.7)
Среднее количество информации в сообщении, вырабатываемом на отрезке наблюдения, составит
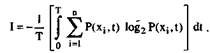 (8.8)
(8.8)
Нахождение вероятностей Р (х;, t) является специфической задачей и определяется типом и характером протекания процесса управления, а также теми требованиями, которые предъявляются к деятельности оператора.
Энтропия сообщения и определяемое ею количество информации определяется по формулам (2.2) и (2.3). Как уже отмечалось, эти формулы оценивают энтропию взаимно независимых сообщений. Иными словами, предполагается, что появление того или иного сообщения не изменяет вероятность появления следующего сообщения. Однако при работе оператора в СЧМ такой случай не всегда возможен. Как правило, поступающая последовательность сигналов обладает логической избыточностью. Это означает, что появление определенного сигнала изменяет вероятность появления следующего сигнала. Наличие логической избыточности равносильно уменьшению энтропии, поскольку появление определенного сигнала X j уменьшает неопределенность очередного состояния информационной модели.
При подсчете количества поступающей в этом случае информации необходимо пользоваться формулами условий энтропии. Так, например, энтропия второго и третьего порядка равна
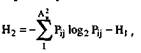 (8.9)
(8.9)
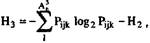 (8.10)
(8.10)
где 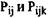 — вероятности появления всех возможных
— вероятности появления всех возможных
диграмм и триграмм сигналов (совместного появления двух и трех сигналов); Hj — энтропия первого порядка, определяемая по формуле 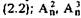 — максимально возможное число диграмм и триграмм сигналов, равное числу размещений по два и по три из общего числа n сигналов.
— максимально возможное число диграмм и триграмм сигналов, равное числу размещений по два и по три из общего числа n сигналов.
Формула (8.9) выражает среднюю энтропию сигнала при условии, что уже известен предыдущий, формула (8.10) — энтропию сигнала, если известны два предыдущих. Подобным образом можно вычислить и энтропию более высоких порядков [119].
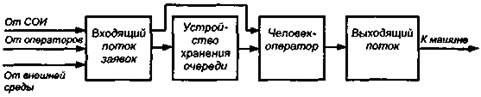
Рис. 8.6. Структурная схема системы массового обслуживания с человеком-оператором.
Для построения моделей деятельности оператора может использоваться также математический аппарат теории массового обслуживания. Структурная схема системы массового обслуживания. (СМО) с человеком-оператором показана на рис. 8.6. Информация со средств отображения и от взаимодействующих операторов, а также сигналы внешней среды образуют входящий поток заявок (требований на обслуживание). Обычно предполагается, что входящий поток подчинен закону Пуассона. Такой поток иначе называется простейшим. Для его описания требуется знать величину X — плотность входящего потока, которая равняется числу заявок, поступивших в единицу времени. Заявки поступают или прямо к оператору, или становятся в очередь на обслуживание (если оператор занят обслуживанием предыдущей заявки). Устройством для хранения очереди могут быть средства отображения информации или память оператора. В зависимости от организации очереди могут быть различные типы СМО: с ожиданием, или без потерь (любая заявка хранится до тех пор, пока не будет обслужена оператором); с ограниченным ожиданием (заявка хранится в очереди ограниченное время); с ограниченной длиной очереди (в очередь может становиться лишь ограниченное число заявок); с потерями (заявки, поступившие в момент занятости оператора, в очередь не становятся и к обслуживанию не принимаются).
Организация очереди определяется характером деятельности оператора. Поэтому при проектировании деятельности следует стремиться, чтобы она, насколько это возможно, была организована по схеме массово-
го обслуживания с ожиданием. При прочих равных условиях это позволяет обеспечить максимальную эффективность функционирования СЧМ.
Заявки, поступившие к оператору, обрабатываются им по заданному алгоритму. Качественная сторона обслуживания (правильно или неправильно обработана информация, с какими затратами сил и средств, какой психофизиологической «ценой» и т. п.) в теории массового обслуживания не учитывается: здесь значение имеет факт поступления или непоступления заявки на обслуживание.
Таким образом, в данной модели оператор представляется в качестве обслуживающего аппарата СМО. Основной его характеристикой является время обслуживания, в теории массового обслуживания оно обычно принимается подчиненным экспоненциальному закону распределения. Для построения закона распределения необходимо знать интенсивность обслуживания μ, которая является величиной, обратной среднему значению времени обслуживания.
Характер обслуживания заявок может быть одноканальным или многоканальным, однофазным или многофазным. При многоканальном обслуживании входящий поток распределяется между несколькими операторами. При многофазном обслуживании поступившая заявка обслуживается аппаратом первой фазы (первым оператором), затем передается на дальнейшее обслуживание во вторую фазу (следующему оператору) и т. д.
Применение аппарата теории массового обслуживания позволяет учесть ряд специфических особенностей, характерных для деятельности оператора и обусловленных представлением его в качестве обслуживающего аппарата. Так, например, ограниченность объема оперативной памяти заставляет рассматривать СМО с ограниченной длиной очереди, а ограниченность длительности сохранения информации в памяти — СМО с ограниченным временем ожидания. Групповая деятельность операторов может быть учтена при рассмотрении многоканальных или многофазных СМО в зависимости от вида взаимодействия операторов.
Возможность совершения ошибок оператором и их исправления приводит к необходимости рассмотрения СМО с ненадежным обслуживающим аппаратом. При этом ошибки оператора рассматриваются как поток отказов обслуживающего аппарата, а время их исправления — как время восстановления.
Применение теории массового обслуживания позволяет решить многие вопросы организации деятельности человека-оператора. К их числу относится определение необходимого числа операторов, определение требований к уровню подготовленности оператора (обученности, скорости реакций, объему памяти и т.д.), определение допустимой плотности потока сигналов, поступающих к оператору, решение некоторых задач организации взаимодействия операторов. Представляется возможность вычисления вероятностей различных состояний системы «человек-машина». Следовательно, так же как и теория информации, теория массового обслуживания дает количественные методы описания деятельности человека-оператора.
К сожалению, применение методов теории массового обслуживания для построения моделей деятельности оператора также связано с целым рядом трудностей. Основная из них определяется введением целого ряда ограничений относительно вида входящего потока заявок и закона распределения времени обслуживания. Входящий поток на практике часто отличается от простейшего, а закон распределения времени обслуживания — от экспоненциального. Другая трудность связана с тем, что в теории массового обслуживания не учитывается качественная, содержательная сторона обслуживания. Для оценки качества обслуживания необходимо дополнительно применять другие методы.
Эти трудности ограничивают область применения аналитических методов теории массового обслуживания. Однако так же, как для теории информации, это не должно являться причиной для полного отказа от применения этих методов в инженерной психологии. Условия их применения здесь сводятся к следующему:
■ поступающая к оператору информация должна допускать интерпретацию ее в терминах входящего потока заявок;
■ входящий поток и время обслуживания должны подчиняться определенным законам распределения;
■ входящий поток должен быть однородным, в противном случае должно быть возможным разделение его на однородные группы (по срочности, важности, затратам на обслуживание и т. п.);
■ для отражения динамического характера процесса обслуживания должна быть установлена система критериальных временных функций, позволяющая оценить эффективность СМО на нестационарных режимах работы.
При соблюдении этих условий возможно применение методов теории массового обслуживания для анализа деятельности оператора в СЧМ [70, 113, 155, 162, 168].
Для построения математических моделей деятельности-оператора в системах непрерывного типа (транспортные средства: самолет, автомобиль, корабль; системы, в которых оператор выполняет функции слежения или наведения; системы регулирования параметров, работающие с участием человека, и т. п.) могут применяться методы теории автоматического управления (ТАУ). С позиций ТАУ человек-оператор рассматривается как элемент следящей системы, какой представляется в данном случае система «человек-машина». На работу системы влияют динамические связи элементов системы друг с другом и человеком.
Процесс анализа системы состоит из трех этапов:
■ установление критерия поведения замкнутой системы и определение ее передаточной функции;
■ нахождение такой передаточной функции оператора, которая позволила бы получить требуемую функцию всей системы;
■ проведение системы мероприятий (отбор, тренировка операторов, соответствующее оформление технической части СЧМ), обеспечивающих требуемую функцию оператора.
При решении этих задач необходимо учитывать следующие психофизиологические особенности человека: ограниченность полосы пропускания, одноканальность, недостаточную точность работы, нестабильность коэффициента усиления, внесение помех и т. п. Как правило, учесть все эти особенности бывает трудно, поэтому на практике используют лишь упрощенные модели деятельности оператора. Одной из них является линейная модель, структурная схема ее показана на рис. 8.7.
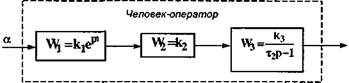
Рис. 8.7. Структурная схема линейной модели.
На этой схеме оператор представляется в виде трех последовательно соединенных звеньев. Первое звено осуществляет прием сигналов; по своим динамическим свойствам оно является усилительным звеном с запаздыванием. Второе звено — решающее (вычислительное). При достаточной тренировке, отсутствии возмущающих воздействий и минимальной психофизиологической напряженности оператора это звено представляет собой обычный усилитель. Третье звено оператора — исполнительное. По своим свойствам оно является инерционным звеном.
Общая передаточная функция такой модели оператора может быть записана как произведение передаточных функций отдельных звеньев
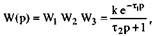 (8.11)
(8.11)
где k = k1k2K3 — коэффициент усиления оператора;
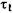 — время реакции оператора, равное в среднем 0,2 с;
— время реакции оператора, равное в среднем 0,2 с;
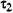 — постоянная времени, характеризующая инерцию (примерно 0,125 с) в образовании исполнительного действия.
— постоянная времени, характеризующая инерцию (примерно 0,125 с) в образовании исполнительного действия.
Наиболее важным недостатком существующих моделей, основанных на использовании аппарата ТАУ, является их линейность. Между тем хорошо известно, что человек-оператор является сугубо нелинейным звеном следящей системы. Для удовлетворительного описания деятельности оператора с учетом этого замечания необходимо применение градиентных методов.

Дата добавления: 2017-08-01; просмотров: 425;
