Элементы теории вероятностей и математической статистики
Случайной величиной называется величина, которая в результате опыы может принять то или иное значение. Случайные величины могут быть дискретными (фиксированными) или непрерывными, принимающими любое зна чение в заданном интервале.
Вероятность события — это численная мера объективной возможности это го события. Она изменяется от нуля (невозможность события) до 1 (достоверность события). Если ввести понятие относительной частоты (частости) события кап отношение числа случаев n благоприятствующих событию i, ко всем наблюдавшимся случаям (n), то вероятность i-го события находится по формуле
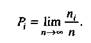
Сумма вероятностей всех возможных событий г равна 1, т.е.
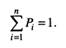
При достаточно большом значении п относительная частота достаточно правильно отражает (оценивает) значение вероятности события. Суммарная
вероятность 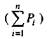 распределена определенным образом между отдельными
распределена определенным образом между отдельными
1-ми событиями. Случайная величина полностью задана, если известно ее распределение. Законом распределения называется соотношение между возможными значениями случайной величины и соответствующими им вероятностями. Простейшей формой задания закона распределения дискретной случайной величины служит таблица, в которой перечислены все значения х, и р,
| х\ | Х\ | х2 | хп | |
| р. | Р\ | Рг | Рп |
Указанная таблица называется рядом распределения.-< Для наглядности ряд распределения часто изображается графически. Для I этого по оси абсцисс откладывают возможные значения случайной величины, I а по оси ординат — вероятности этих значений. Полученная геометрическая фигура (рис. 4.3) называется многоугольником (полигоном) распределения.
Иногда удобна «механическая» интерпретация ряда распределения. Это некоторая масса, равная 1 и распределенная по оси х так, что в отдельных точках х\, х2, ..., х„помещены соответствующие массы Р{, Р2, …, Р„-
Для количественной характеристики распределения непрерывной случайной величины удобно пользоваться не вероятностью данного события Х = х, а I вероятностью события X < х, где х — текущая переменная. Вероятность события ■ X < х величина переменная, функция от х. Эта функция называется функцией I распределения случайной величины Xи обозначается Р(х): Р{х) = Р(Х<х).
Свойства плотности распределения:
а) плотность распределения неотрицательная функция:Лх)> 0;
б) интеграл в бесконечных пределах от плотности вероятности равен
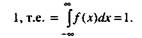
Величина Р(х) безразмерная, а Ддс) имеет размерность, обратную случай ной величине.
Гистограмма — это статистический ряд, оформленный графически. Для построения гистограммы на оси абсцисс откладываются интервалы и на каж дом из интервалов, как на основании, строится прямоугольник, площадь кото рого равна относительной частоте данного разряда. Для построения гисто граммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника (рис. 4.5).
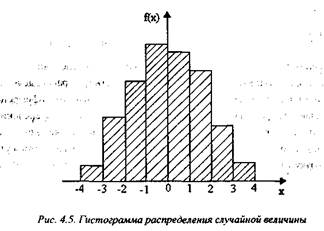 |
Этот график представляет собой плотность распределения случайной вели чины X. Интервалы для построения гистограмм выбираются произвольно, но для определения оптимальной величины интервала можно применять формулу
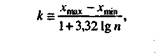
|
где (хтах - хт\„) — размах изменения случайной величины; п — число наблюдений в выборке.
В качестве основных числовых характеристик применяется математическое ожидание, дисперсия, асимметрия, эксцесс.
Математическим ожиданием случайной величины называется сумма произведений значений случайной величины на вероятность этих значений:
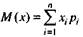
|
(при достаточно больших п математическое ожидание может
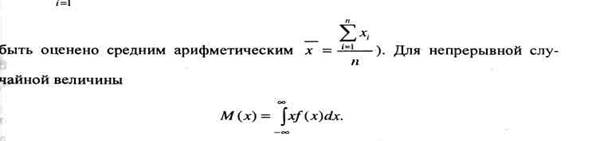
Свойства математического ожидания:
а) М(с) = с;
б) М(сх) = сМ(х)\
в) М(х+у) = М(х) + Л/О);
г) М{ху) = М(х)М(у).
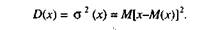
|
| Для дискретных величин |
Дисперсией (рассеиванием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
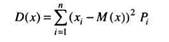
|
и для непрерывных случайных величин
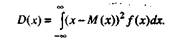
|
Дата добавления: 2017-06-02; просмотров: 863;
