Продолжение примера 61.
Для нахождения коэффициента Ь0 уравнения регрессии (4.2) вычисляем сумму произведений yt на значение фиктивной переменной х0 (+1) и делим ре-зультат на N= 4 (при к - 3 делить на N = 8).
'. 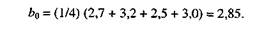
Для вычисления Ь\ по формуле (4.4) вычисляем сумму произведений у-, на соответствующие значения Х\ (+1 или -1), и подобным образом поступаем при определении Ь2 и Ъп (в последнем случае yv умножим на значение xix2) (см. табл. 4.3): 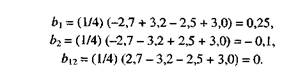
Таким образом, в рассматриваемом примере уравнение регрессии
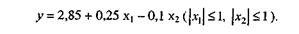 (4.5)
(4.5)
Коэффициент Ъп характеризует взаимодействие между факторами, т.е. показывает, что влияние одного фактора зависит от значения другого. В данном условном примере bi2 = 0, что свидетельствует об отсутствии взаимодействия между 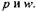
Уравнение (4.5) может быть представлено в натуральных значениях, для
чего необходимо заменить х на 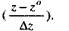 В данном случае
В данном случае
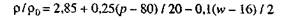
или 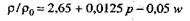
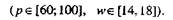
После получения уравнения регрессии (4.5) необходимо провести статистическую оценку значимости найденных величин. Вместе с тем, уже само уравнение (6.5) показывает, что при изменении ре [60; 100] степень прессования р/р0 вырастает на 0,5 (±0,25), а при увеличении w= [14,18] р/р9
уменьшится (Ь2 < 0) на 0,2 (+ 0,1).
Оценка значимости коэффициентов регрессии bj проводится по выборочной дисперсии S2 (bj). Коэффициенты регрессии вычисляют по средним значениям у; (не менее трех повторностей (т > 3) опытов по каждой строке ПФЭ).
Таблица ц Опытные данные при трехкратной повторности опытов р/Ро =fip, hi)
| Номер варианта | Х\ | х2 | у,-(1) | (2)У! | уР | У< |
| - | - | 2,5 | 2,6 | 3,0 | 2,7 | |
| + | - | 3,1 | 3,2 | 3,3 | 3,2 | |
| - | + | 2,4 | 2,6 | 2,5 | 2,5 | |
| + | + | 3,2 | 2,8 | 3,0 | 3,0 |
Расчет выборочной дисперсии ведут по формуле
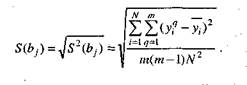
В табл. 4.4 представлены результаты трехкратной повторности опытов ц0 матрице (см. табл. 4.3).
Вычисляем выборочную дисперсию S (bj):
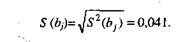
|
Для оценки значимости коэффициентов регрессии составляем неравенство
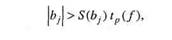
где S (bj) — ошибка коэффициента регрессии; t (f) — коэффициент Стьюдента, находимый из специальных таблиц для заданной вероятности Р и числа
Дата добавления: 2017-06-02; просмотров: 530;
