Линейное программирование в задачах управления производством

Многие задачи управления, экономики и организации производства решаются с использованием метода линейного программирования.

Модель линейного программирования состоит из совокупности линейны» алгебраических уравнений и неравенств, выражающих функцию цели и oграничения на нее. Математическая модель линейного программирования в общем случае имеет следующий вид:

■■'■'•■

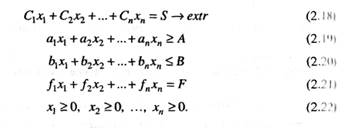
При решении задач на минимум (2.18) преобладают ограничения типа (2.19), а на максимум — типа (2.20); в транспортных задачах преобладают oграничения в виде равенств (2.21). В общем случае в любой из перечисленные задач могут встретиться ограничения всех трех типов.

Решение задач типа (2.18)-(2.22) составляет предмет линейного программирования. В практических задачах критерий оптимизации 5(2.18) чаще всех является экономическим (приведенные затраты, прибыль, себестоимость), но применяются и технологические показатели (число часов работы, площадь производительность и др.);

x_i,x₂,-.,x_n — искомые неотрицательные переменые, имеющие различный смысл в задачах (объем производства, число часе и работы машин, планируемые под разработку площади, количество компонентов в смеси и т.д.). Дополнительные условия (2.19)—(2.21) представляют собой ограничения на функцию цели (2.18) по материальным и сырьевым ресурса' производственным заданиям, мощностям, трудоемкости, капитальным затратам, соотношениям различных технологий, удельных расходов и затрат.

Приведем ряд задач горного производства, решенных методом линейного программирования. К их числу относятся задачи оценки запасов сырьевых баз - позиций оптимального удовлетворения потребностей проектируемых пред-приятий в сырье, оптимизации использования сырьевых ресурсов при их ком-дакеной переработке на основе малоотходной технологии, оптимизации распределения технологического оборудования в цикле с целью улучшения каче­нии добываемой продукции и экономики производства, транспортные задачи оптимального распределения продукции, баланса топлива и ряд других. Уже их перечень указывает на их масштабность и важность для улучшения эко-Иимики горной отрасли. Эффективность задач линейного программирования высока. Например, эффективность оптимального планирования распределения торфяных брикетов в Беларуси, выполненного в Белорусском политехниче-ском институте в 80-х годах, определилась снижением грузопотока на 6%, что в масштабе республики дало за год экономию нескольких миллионов тоннокилометров перевозок. В различных регионах страны транспортные расходы в оптимальном варианте могут быть снижены на 10-30%.

Функция (2.18) критерия оптимизации S, экстремум которой отыскивается, называется целевой или функцией цели. Совокупность х₁,х₂,..-,х_п, удов­летворяющих ограничениям (2.19)-(2.22), называется областью допустимых Ьрчений переменных или допустимой областью решений. Набор ^ _чх_г,...,х_п , при которых целевая функция (2.18) принимает наибольшее или наименьшее значение, — решением задачи линейногопро программирования или оптимальмым планом.

Задача оптимизации при ограничениях (2.19)-(2.22) может не иметь ни одного допустимого решения или одно (несколько) множество оптимальных решений. Экстремум может находиться лишь где-то на границе области, а не внутри. В большинстве задач линейного программирования искомыми являются Переменные, число которых достигает десятков, сотен и даже тысяч. В таких случаях необходимо применение ЭВМ. Однако многие практические задачи Могут быть решены и ручными методами. В случае двух искомых переменных задача линейного программирования может быть легко решена геометрическим методом.

13 Динамическое программирование

Динамическое программирование (планирование) применяется для нахо-дения оптимальных решений в многошаговых (многоэтапных) задачах. Принцип оптимальности динамического программирования сформулирован Р. Веллманом: «Оптимальное поведение обладает тем свойством, что каковы бы ИИ были первоначальное состояние и решение в начальный момент, после­дующие решения должны составлять оптимальное поведение относительно Состояния, полученного в результате первоначального решения».

Примерами задач, решаемых методом динамического программирования, могут служить:

• планирование производственной программы по периодам года при минимальных затратах на производство и содержание запасов;

• оптимальное распределение средств и ресурсов на расширение производства при максимизации прироста выпуска продукции;

• оптимальное планирование замены устаревшего оборудования бо­лее совершенным при максимизации прибыли;

• календарное планирование ремонта либо замены устаревшего обо­рудования при минимуме эксплуатационных затрат;

• выбор оптимального маршрута при минимуме транспортных рас­ходов и т.д.

Любую многоэтапную задачу можно решать двумя способами: искать оп­тимальное решение сразу на всем протяжении процесса или строить его шаг за шагом. После оптимизации (-го шага, исходя из результатов предыдущего, оптимизируют следующий (« + 1)-й шаг. Второй способ проще. Его суть в по­степенной, поэтапной оптимизации, что особенно ценно в задачах, где ситуа­ция меняется во времени, и поэтому необходимо планировать с учетом вре­менного фактора.

Принцип оптимальности Беллмана записывается в виде рекуррентного соотношения

/„-,(*,) = max(min)| R_M (*,., х_м) + f_nHM){x_i+l)\,