Нормальный закон распределения.

Нормальный закон распределения получил широкое применение в практической метрологии, что объясняется центральной предельной теоремой теории вероятностей (теоремой Ляпунова), согласно которой распределение случайных погрешностей будет близко к нормальному во всех случаях, когда результаты наблюдений формируются под влиянием большого числа независимых факторов, каждый из которых оказывает незначительное действие по сравнению с суммарным действием остальных.

Нормальный закон распределения характеризуется свойствами:

- погрешность может принимать непрерывный ряд значений от 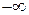до ;

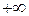- равные по абсолютному значению погрешност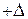и и 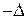равновероятны;

- малые по абсолютному значению погрешности более вероятны, чем большие.

Нормальный закон распределения описывается выражением

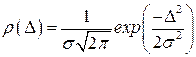, (2.9)

где 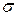- среднеквадратическое отклонение погрешности .

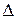График нормального закона распределения представлен на рисунке 2.1.

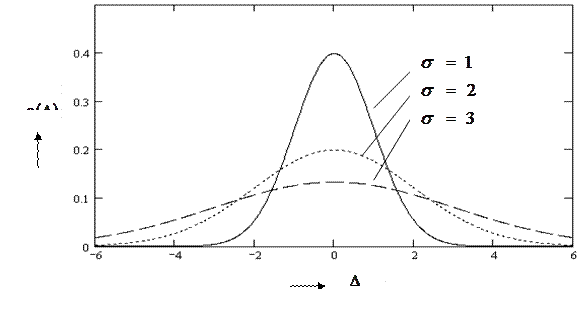
Рисунок 2.1 – График нормального закона распределения плотности

вероятности случайных погрешностей

Из графиков следует, что центр распределения находится в нуле, т.е. в точке нулевой погрешности 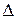. По мере удаления от центра распределения вероятность появления погрешности 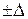уменьшается. Чем больше 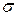, тем выше вероятность появления более точных результатов измерений, о чем говорит более высокий уровень максимума при большем .

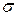В теории вероятностей часто используется понятие дисперсия D, характеризующая рассеяние погрешностей относительно центра распределения

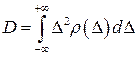. (2.10)

Дисперсия D связана с среднеквадратическим отклонением 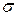соотношением

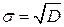. (2.11)

Для определения вероятности 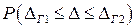при нормальном законе распределения случайной погрешности 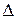необходимо вычислить интеграл

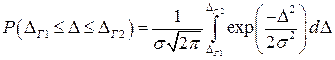. (2.12)

Для симметричного интервала распределения погрешностей от 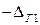до будем иметь

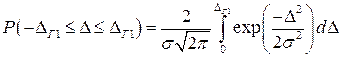. (2.13)

Если в подинтегральном выражении вероятности 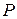заменить погрешность 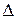на относительную 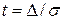, получим нормированный нормальный закон распределения плотности вероятностей

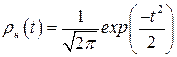. (2.14)

График нормированного нормального закона распределения соответствует нормальному закону распределения, приведенному на рисунке 2.1 при .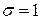

На практике часто используют интеграл вероятностей 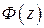, который численно равен вероятности 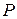при интегрировании нормированного нормального закона распределения плотности вероятностей в пределах от нуля до z, где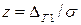

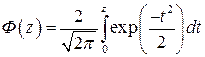. (2.15)

Значения интеграла вероятностей 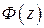в зависимости от пределов интегрирования приведены в таблице 2.1. Пользуясь таблицей значений интеграла вероятностей 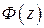можно выполнять вычисления интервала погрешности измерений по заданной вероятности или вероятности по заданным границам погрешности измерений.

Для оценки погрешности измерений используют среднеквадратическое отклонение 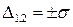, равновероятную ( 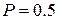) погрешность 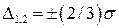, максимальную ( 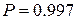) погрешность .

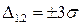Таблица 2.1 - Значения интеграла вероятностей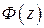

z		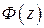z		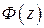z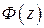
0.00	0.000	0.80	0.576	1.80	0.928
0.20	0.159	1.00	0.683	2.00	0.955
0.40	0.311	1.20	0.770	2.33	0.980
0.50	0.383	1.40	0.839	2.58	0.990
0.60	0.452	1.60	0.89	3.00	0.997

Пользуясь таблицей значений интеграла вероятностей 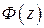можно выполнять вычисления интервала погрешности измерений по заданной вероятности или вероятности по заданным границам погрешности измерений.

Нормальный закон распределения применяют для обработки результатов измерений при числе повторных измерений больше 20.