Обработка результатов косвенных измерений

При косвенных измерениях искомая величина 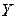является функцией ряда других величин - аргументов .

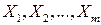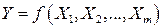. (2.38)

Результат косвенных измерений оценивается погрешностью 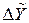, которая определяется погрешностями аргументов 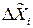, где , и наличием статистической связи (корреляции) между аргументами.

Представим погрешности аргументов 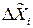в виде систематической и случайной 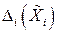составляющих

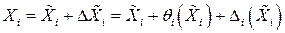. (2.39)

Тогда результат косвенных измерений можно представить через погрешности аргументов

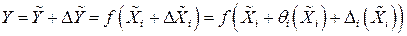. (2.40)

Разложим функцию в ряд Тейлора, отбросим отклонения выше первого порядка и выразим результат через среднеарифметические значения и погрешности аргументов

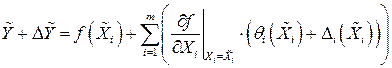, (2.41)

где 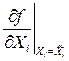- коэффициент влияния i – го аргумента;

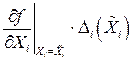- частная погрешность i – го аргумента.

Из формулы (2.41) получаем выражение для оценки результата косвенного измерения

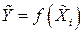, (2.42)

а также выражения для оценки систематической 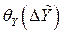и случайной 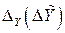погрешностей результата косвенного измерения

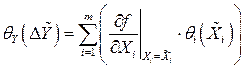; (2.43)

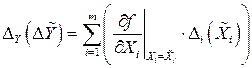. (2.44)

Из выражения (2.44) можно найти приближенное выражение для оценки среднеквадратического отклонения 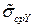случайной погрешности результата косвенного измерения в зависимости от оценок среднеквадратических отклонений случайных погрешностей аргументов

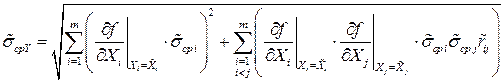, (2.45)

где 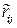- оценка коэффициента корреляции, определяющая меру статистической связи случайных величин 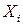и .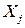

Все возможные оценки коэффициента корреляции 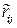лежат в интервале от -1 до +1. Установить значение 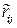обычно затруднено, поэтому рассматривают два случая: 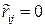(отсутствие статистической связи) и 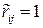(полная статистическая связь).

При 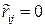формула (2.45) преобразуется к виду

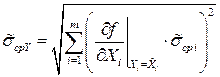, (2.46)

т.е. оценки среднеквадратических отклонений случайных погрешностей аргументов суммируются геометрически как независимые случайные.

При 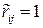формула (2.45) преобразуется к виду

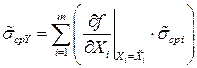, (2.47)

т.е. оценки среднеквадратических отклонений случайных погрешностей аргументов суммируются алгебраически с учетом знаков.

Результат косвенных измерений записывается в соответствии с выражением (2.24), т.е. также как и при прямых измерениях, но доверительный интервал 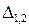вычисляется с учетом оценок среднеквадратических отклонений случайных погрешностей аргументов и оценок коэффициентов корреляции 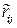между ними.