Обработка результатов совместных измерений

В практике измерений часто возникает необходимость в экспериментальном определении зависимости между двумя или большим числом измеряемых физических величин. Предположим, что между физическими величинами x и y имеет место аналитическая зависимость, которую представим выражением

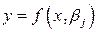, (2.48)

где 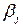- неизвестные коэффициенты, .

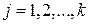В результате измерений можно получить n экспериментальных точек с координатами 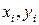на координатной плоскости XOY, причем 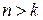. По расположению экспериментальных точек на координатной плоскости можно сделать предположение о виде аппроксимирующей функции. Ее можно представить какой-либо конкретной функцией, например, синус, тангенс, логарифм, экспонента, арктангенс и др. или полиномом высокой степени. В общем виде аппроксимирующую функцию представим в виде

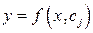, (2.48)

где 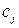искомые коэффициенты аппроксимирующей функции, .

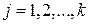Необходимо определить коэффициенты 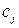, используя результаты измерений, выполненные с некоторой погрешностью. Будем считать, что погрешность измерений носит случайный характер и подчиняется нормальному закону распределения плотности вероятности случайных погрешностей. Для решения подобных задач наибольшее распространение получил метод наименьших квадратов.

Погрешности измерения, а также неточный выбор аппроксимирующей функции являются причиной возникновения погрешности между вычисленным значением функции 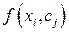по измеренному значению аргумента 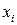и измеренным значением функции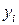

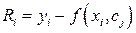. (2.49)

В соответствии с методом наименьших квадратов аналитическая зависимость будет наилучшим образом описывать экспериментальную, если сумма квадратов погрешности 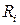будет минимальна.

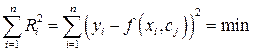. (2.50)

Для вычисления 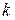неизвестных коэффициентов 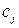необходимо записать систему 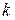уравнений

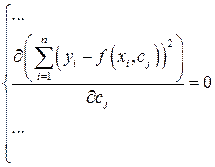. (2.51)

Или после преобразований в развернутом виде

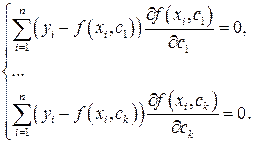(2.52)

Приведенная система уравнений достаточно просто решается в системе MathCad. Средствами MathCad может быть организована и вся процедура вычисления коэффициентов аппроксимирующей функции по методу наименьших квадратов.