Определение напряжений в осесимметричных оболочках по безмоментной теории

Оболочками называют тела, толщина которых значительно меньше двух других измерений. Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, называется срединной поверхностью. Если срединная поверхность образует часть сферы, конуса или цилиндра, оболочку соответственно называют сферической, конической или цилиндрической. Толщина оболочки может изменяться по какому-то закону или оставаться постоянной.

Осесимметричными оболочками называют такие, срединная поверхность которых представляет собой поверхность вращения, т.е. образуется в результате вращения плоской кривой вокруг прямой линии, называемой осью и лежащей в той же плоскости (рис. 4.1).

Задача о расчете оболочек вращения решается значительно проще в том случае, когда можно принять, что напряжения в оболочке постоянны по толщине. Соответственно в этом случае будут отсутствовать изгибающие моменты. Теория, построенная на таком предположении, называется безмоментной теорией оболочек. Такие оболочки работают только на растяжение-сжатие и являются наиболее прочными и жесткими. В связи с этим при проектировании несущих оболочечных конструкций необходимо стремиться обеспечить их работу как безмоментных.

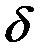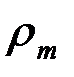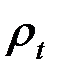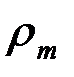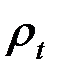Рассмотрим осесимметричную оболочку толщиной (рис. 4.1). Обозначим через радиус кривизны дуги меридиана срединной поверхности (рис. 4.1, а), а через – второй главный радиус или радиус кривизны нормального сечения перпендикулярного к дуге меридиана. Этот радиус равен отрезку нормали между поверхностью оболочки и осью симметрии. В общем случае величина радиусов кривизны и является функцией угла 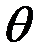между нормалью и осью симметрии.

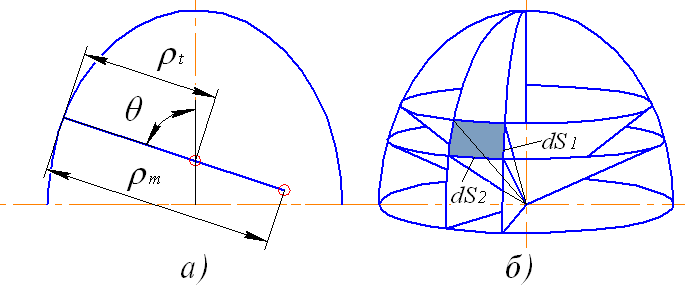
Рис. 4.1. Схема осесимметричной оболочки

Выделим на поверхности оболочки элемент с размерам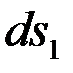и и
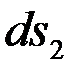двумя меридианальными и нормальными коническими сечениями
(рис. 4.1, б).

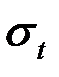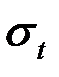На гранях этого элемента возникают напряжения и (рис. 4.2, а). Напряжение называется окружным, а напряжение – меридианаль­ным и его вектор направлен по дуге меридиана.

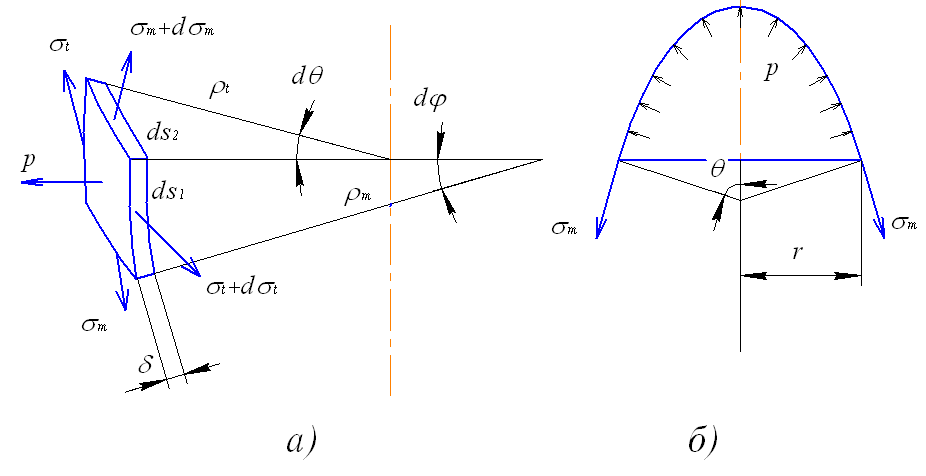
Рис. 4.2. Расчетная схема для определения напряжений
в безмоментной оболочке

Составим уравнение равновесия выделенного элемента. На его гранях возникают силы

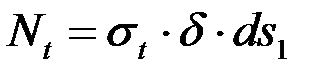и 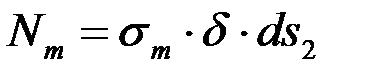. (4.1)

Внутреннее давление создает силу по нормали к элементу, равную 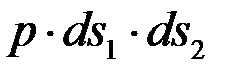. Составим сумму проекций этих сил на нормаль, не учитывая слагаемые второго порядка малости от напряжени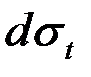й и :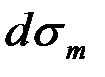

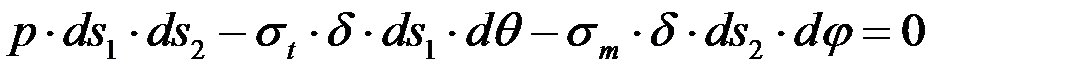. (4.2)

Учитывая геометрические соотношения

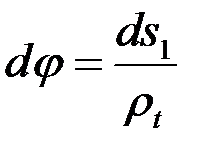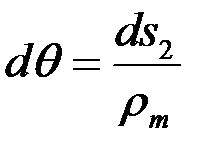; , (4.3)

окончательно получаем

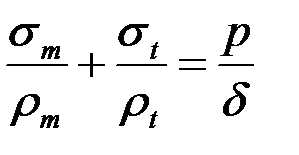. (4.4)

Это соотношение носит название уравнения Лапласа.

Так как в уравнение Лапласа входят два неизвестных напряжения, необходимо составить ещё одно уравнение проекций сил на направление оси оболочки. При этом удобнее составлять такое соотношение не для элемента, а для части оболочки, отсеченной коническим нормальным сечением (рис. 4.2, б). Для того, чтобы правильно использовать такое уравнение равновесия, необходимо помнить следующую теорему.

Если на какую-то поверхность действует равномерно распределенное давление, то, независимо от формы этой поверхности, проекция равнодействующей сил давления на заданную ось равна произведению давления 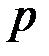на площадь проекции поверхности на плоскость, перпендикулярную к заданной оси.