Уравнения состояния реального газа.

Наиболее простым и качественно верно отображающим поведение реального газа, является уравнение Ван-дер-Ваальса:

(P + a/n²)·(n – b) = R·T . (6.3)

а, b – постоянные величины, первая учитывает силы взаимодействия, вторая учитывает размер молекул.
a/n² – характеризует добавочное давление, под которым находится реальный газ вследствие сил сцепления между молекулами и называется внутренним давлением. Для жидких тел это давление имеет большие значения (например, для воды при 20⁰С составляет 1050 Мпа), а для газов из-за малых сил сцепления молекул оно очень мало. Поэтому внешнее давление, под которым находится жидкость, оказывает ничтожное влияние на её объем, и жидкость считают несжимаемой. В газах в виду малости значения a/n² внешнее давление легко изменяет их объем.
Уравнение Ван-дер-Ваальса качественно верно отображает поведение жидких и газообразных веществ, для двухфазных состояний оно неприменимо.
На PV – диаграмме (рис.6.1) показаны изотермы построенные по уравнению Ван-дер-Ваальса. Из кривых видно, что при сравнительно низких температурах имеются волнообразные участки. Чем выше температура, тем короче эти части кривых. Эти волнообразные кривые указывают на непрерывный переход от жидкого состояния в парообразное при данной температуре. Точка А соответствует состоянии жидкости, точка В относится парообразному состоянии вещества.

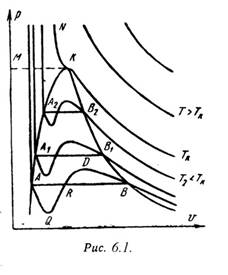
В действительности переход из жидкого состояния в парообразное всегда происходит через двухфазное состояние вещества. При этом при данной температуре процесс перехода происходит также и при постоянном давлении. Этот действительный переход из жидкого состояния в парообразное изображается прямой линией АВ.
Практически для особо чистых веществ возможно осуществление участков волнообразной кривой AQ и DB. В первом случае имеют место неустойчивые состояния перегретой жидкости, а во втором – переохлажденного пара.
При определенной температуре изотерма уравнения Ван-дер-Ваальса не будет иметь волнообразного участка (точка К). Эту температуру называют критической. Если соединить точки А₁, А₂, А₃ … и В₁, В₂, В₃ ... получим кривую похожую на параболу. Кривая АК называется нижней пограничной кривой и соответствует в состоянии кипения жидкости. Кривая КВ называется верхней пограничной кривой и соответствует состояния сухого насыщенного пара.
Таким образом, для реального вещества PV – диаграмму можно разбить на 3 области:
1 - область жидкого состояния, расположена левее нижней пограничной кривой;
2 - область двухфазных состояний (влажный пар), расположена между нижней и верхней пограничной кривой);
3 – область перегретого пара, расположена правее верхней пограничной кривой и выше критической точки. Условно область жидкости ограничивают сверху линией КМ – критическая изобара.
Критическую температуру Д.И.Менделеев называл абсолютной температурой кипения, при которой поверхностное натяжение в жидкости становится равным нулю, т.е. исчезает различие между жидкостью и парообразным состоянием вещества (насыщенным паром).
Связь между критическими параметрами и постоянными уравнения Ван-дер-Ваальса:

Т_к = 8·а/(27·R·b) ; P_к = a/(27·b²) ; (6.4)
а = (27· R² ·Т²_к)/(64 ·P_к) ; b = (27· R ·Т_к)/(8 ·P_к). (6.5)

Уравнение Ван-дер-Ваальса при больших плотностях газа дает значительные ошибки. Кроме этого экспериментальным путем доказана, что коэффициенты а, b зависят от температуры и давления, причем эта зависимость очень сложная.
М.П.Вукалович и И.И.Новиков в 1939 г. предложили новое универсальное уравнение состояния реальных газов с учетом ассоциации и диссоциации их молекул, который имеет следующий вид:

(P + a/n²)·(n – b) = R·T (1 – С/( n ·Т^(3+2m)/2), (6.6)

где a, b – постоянные уравнения Ван-дер-Ваальса;
С, m – постоянные, определяемые на основании опытных данных.