Критическое давление и скорость. Сопло Лаваля.

Если перемещение газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называется соплом.
Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называют диффузором.
В каналах при небольшой разности давлений газа и внешней среды скорость течения рабочего тела достаточно большая. В большинстве случаев длина канала небольшая и процесс теплообмена между стенкой и газом незначителен, поэтому процесс истечения газа можно считать адиабатным.
Скорость истечения (на выходе канала) определяется из уравнения:

w = w₂ = v 2(h₁ – h₂) . (5.6)

или

w = v 2Ö/(g - 1)·P₁·х ₁ [1 – (P₂/P₁)^(g-1)/g]. (5.7)

Массовый секундный расход газа, [кг/с]:

m = f·w/х ₂ , (5.8)

где: f – площадь сечения канала на выходе.
Так как процесс истечения адиабатный, то:

m = f·Ö 2g/(g - 1)·P₁/х ₁·[(P₂/P₁)^2/g – (P₂/P₁)^(g+1)/g]. (5.9)

Массовый секундный расход идеального газа зависит от площади выходного канала, начального состояния газа и степени его расширения.
Критическим давлением называется такое давление на выходном сечении канала, при котором достигается максимальный расход газа и определяется следующим выражением:

P_К = P₂ = b_К·P₁ , (5.10)

где: P_К = (2/(g + 1))^г/(г-1) .
для одноатомных газов: g =1,66 q b_К = 0,49 ;
для двухатомных газов: g =1,4 q b_К = 0,528 ;
для трехатомных газов: g =1,3 q b_К = 0,546 .
Критической скоростью называется скорость газа в выходном сечении канала, при давлении равном или меньшем критического - P_К.

w_К = Ö 2(g/(g + 1))·P₁·х ₁ . (5.11)

Критическая скорость зависит при истечении идеального газа только от начальных параметров, его природы и равна скорости звука газа (а) при критических параметрах.

w_К = а = Ö g·P_К·х_К . (5.12)

Комбинированное сопло Лаваля предназначено для использования больших перепадов давления и для порлучения скоростей истечения, превышающих критическую или скорость звука. Сопло Лаваля состоит из короткого суживающегося участка и расширяющейсяя конической насадки (Рис.5.1). Опыты показывают, что угол конусности расширяющейся части должен быть равен a = 8-12^о. При больших углах наблюдается отрыв струи от стенок канала.

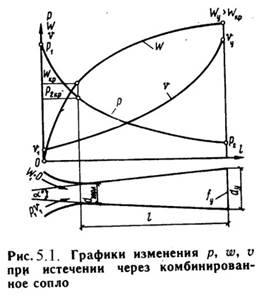
Скорость истечения и секундный расход идеального газа определяются по формулам (5.7) и (5.9).
Длину расширяющейся части сопла можно определить по уравнению:

l = (D – d) / 2·tg(j/2) , (5.13)

где: j - угол конусности сопла;
D - диаметр выходного отверстия;
d - диаметр сопла в минимальном сечении.

Дросселирование.

Дросселированием называется явление, при котором пар или газ переходит с высого давления на низкое без совершения внешней работы и без подвода или отвода теплоты. Такое явление происходит в трубопроводе, где имеется место сужения проходного канала (Рис.5.2). При таком сужении, вследствие сопротивлений, давление за местом сужения - Р₂, всегда меньше давления перед ним – Р₁.

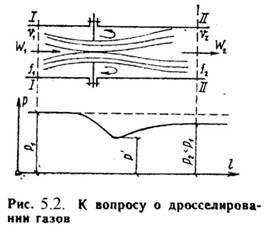
Любой кран, вентиль, задвижка, клапан и прочие местные сопротивления, уменьшающие проходное сечение трубопровода, вызывают дросселирования газа или пара, следовательно падения давления. В большинстве случаев это явление приносит безусловный вред. Но иногда оно является необходим и создается искусственно (регулирование паровых двигателей, в холодильных установках, в приборах для измерения расхода газа и т.д.).
При прохождении газа через отверстие, кинетическая энергия газа и его скорость в узком сечении возрастают, что сопровождается падением температуры и давления.
Газ, протекая через отверстие, приходит в вихревое движение. Часть его кинетической энергии затрачивается на образование этих вихрей и превращается в теплоту. Кроме того, в теплоту превращается и работа, затраченная на преодоление сопротивлений (трение). Вся эта теплота воспринимается газом, в результате чего температура его изменяется (уменьшается или увеличивается).
В отверстие скорость газа увеличивается. За отверстием газ опять течет по полному сечению и скорость его вновь понижается. А давление увеличивается, но до начального значения оно не поднимается; некоторое изменение скорости произойдет в связи с увеличением удельного объема газа от уменьшения давления.
Дросселирование является необратимым процессом, при которм происходит увеличение энтропии и уменьшение работоспособности рабочего тела.
Уравнением процесса дросселирования является следующее уравнение:

i₁ = i₂ . (5.14)

Это равенство показывает, что энтальпия в результате дросселирования не изменяется и справедливо только для сечений, достаточно удаленных от сужения.
Для идеальных газов энтальпия газа является однозначной функцией температуры. Отсюда следует, что при дросселировании идеального газа его температура не изменяется (Т₁ = Т₂).
При дросселировании реальных газов энтальпия газа остается постоянной, энтропия и объем увеличиваются, давление падает, а температура изменяется (увеличивается, уменьшается или остется неизменной).
Изменение температуры жидкостей и реальных газов при дросселировании называется эффектом Джоуля-Томсона. Для идеального газа эффект Джоуля-Томсона равен нулю. Различают дифференциальный температурный эффект, когда давление и температура изменяются на бесконечно малую величину, и интегральный температурный эффект, при котором давление и температура изменяются на конечную величину.
Дифференциальный температурный эффект обозначается - б:

a = (¶T/¶P)_i . (5.15)

Интегральный температурный эффект определяется из следующего уравнения:

DT = T₂ – T₁ = ò [T·(¶n/¶T)_p – n] / c_p dP . (5.16)

Для реальных газов DT¹0 и может иметь положительный или отрицательный знак.
Состояние газа, при котором температурный эффект меняет свой знак, называется точкой инверсии, а температура, соответствующая этой точке, называется температурой инверсии - Т_инв.

Т_инв = n·(¶Т/j¶ n)_p . (5.17)

Тема 6. Реальные газы. Водяной пар. Влажный воздух.