Формализованные методы

Матричные методы.Матричные формы представления и анализа информации не являются специфическим инструментом системного анализа, однако широко используются на различных его этапах в качестве вспомогательного средства. Матрица является не только наглядной формой представления информации, но и формой, которая во многих случаях раскрывает внутренние связи между элементами, помогает выяснить и проанализировать наблюдаемые части структуры. Примером использования свойств матрицы является таблица Менделеева.

Матрицы используются для представления и анализа систем и их структур. Перестроение дерева целей в матрицу бывает удобно для анализа структуры дерева целей, для выявления взаимосвязей и отношений между целями на этапе отбора вариантов и усечения целей.

Сетевые методы.Сетевые методы являются наиболее наглядным и удобным средством отражения динамических, развивающихся во времени процессов, их анализа и планирования с включением элементов оптимизации. Используются главным образом на этапе построения программ развития. Элементы нижних уровней дерева целей, перегруппированные по признаку временных логических взаимосвязей, можно преобразовать в сеть. Анализ этих сетей может послужить для дальнейшей корректировки деревьев целей. Более сложные многомерные сети используются для распределения сфер ответственности, распределения работ по конкретным исполнителям в организациях, ориентированных на цель.

Статистические методы.Величины, которые могут принимать различные значения в зависимости от внешних по отношению к ним условий, принято называть случайными (стохастичнымипо природе). Так, например: пол встреченного нами человека может быть женским или мужским (дискретная случайная величина); его рост также может быть различным, но это уже непрерывная случайная величина - с тем или иным количеством возможных значений (в зависимости от единицы измерения).

Для случайных величин приходится использовать особые, статистические методы их описания. В зависимости от типа самой случайной величины - дискретная или непрерывная это делается по разному.

Дискретное описание заключается в том, что указываются все возможные значения данной величины (например - 7 цветов обычного спектра) и для каждой из них указывается вероятность или частота наблюдений именного этого значения при бесконечно большом числе всех наблюдений.

Можно доказать, что при увеличении числа наблюдений в определенных условиях за значениями некоторой дискретной величины частота повторений данного значения будет все больше приближаться к некоторому фиксированному значению - которое и есть вероятность этого значения.

К понятию вероятности значения дискретной случайной величины можно подойти и иным путем - через случайные события. Это наиболее простое понятие в теории вероятностей и математической статистике - событие с вероятностью 0,5 или 50% в 50 случаях из 100 может произойти или не произойти, если же его вероятность более 0,5 - оно чаще происходит, чем не происходит. События с вероятностью 1 называют достоверными, а с вероятностью 0 - невозможными.

Отсюда простое правило: для случайного события X вероятности P(X) (событие происходит) и P(X) (событие не происходит), в сумме для простого события дают 1.

В ряде ситуаций приходится иметь дело с непрерывно распределенными случайными величинами - весами, расстояниями и т. п. Для них идея оценки среднего значения (математического ожидания) и меры рассеяния (дисперсии) остается той же, что и для дискретных случайных величин. Приходится только вместо соответствующих сумм вычислять интегралы. Второе отличие - для непрерывной случайной величины вопрос о том какова вероятность принятия ею конкретного значения обычно не имеет смысла - как проверить, что вес товара составляет точно 242 кг - не больше и не меньше?

Для всех случайных величин - дискретных и непрерывно распределенных, имеет очень большой смысл вопрос о диапазоне значений. В самом деле, иногда знание вероятности того события, что случайная величина не превзойдет заданный рубеж, является единственным способом использовать имеющуюся информацию для системного анализа и системного подхода к управлению. Правило определения вероятности попадания в диапазон очень просто - надо просуммировать вероятности отдельных дискретных значений диапазона или проинтегрировать кривую распределения на этом диапазоне.

Математическое программирование ("планирование") - это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.

В зависимости от вида целевой функции и ограничений выделяют следующие методы математического программирования:

Линейное программирование, используется если целевая функция линейна и система ограничений также линейна.

Если решения задачи линейного программирования должны быть целыми числами, то это задача целочисленного линейного программирования.

Если целевая функция и система ограничений не линейны, то это задача нелинейного программирования.

В том случае, если в задаче математического программирования имеется переменная времени и целевая функция выражается не в явном виде, как функция переменных, а косвенно, через уравнение, описывающее протекание операции во времени, то такая задача является задачей динамического программирования.
Если целевая функция и система ограничений задаются формулами вида:

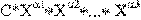,то это задача геометрического программирования.

В задачах параметрического программированияцелевая функция и система ограничений зависят от параметров.

Если в целевой функции и системе ограничений определяется область возможного изменения переменных, содержатся случайные величины, то такая задача относится к задачам стохастического программирования.

Если точный оптимум найти алгоритмическим путем невозможно, из-за большого числа вариантов решения, то используются методы эвристического программирования.

Контрольные вопросы

1. Назовите основные особенности системного анализа.

2. Для каких целей разрабатывается методика системного анализа и в каких случаях она применяется?

3. Опишите метод «мозговой атаки».

4. Опишите методы экспертных оценок.

5. Опишите метод «Дельфи».

6. Опишите диагностические методы.

7. Опишите морфологические методы.

8. Опишите метод дерева целей.

9. Опишите матричные методы.

10. Опишите сетевые методы.

11. Опишите статистические методы.

12. Опишите методы математического программирования.

Тема№8
Применение системного анализа в экономике и управлении