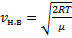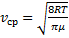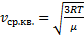Молекулярная физика и термодинамика
Изопроцессы и закономерности их протекания.
Любое изменение в системе, связанное с изменением ее термодинамических параметров, называетсятермодинамическим процессом.
Из уравнения Клапейрона – Менделеева следует, что для данной массы газа 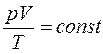 в любом термодинамическом процессе,
в любом термодинамическом процессе,
что является формулировкой объединенного газового закона.
Если в термодинамическом процессе один из параметров газа ( 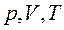 ) не изменяется, то такой процесс называется изопроцессом.
) не изменяется, то такой процесс называется изопроцессом.
Процесс, протекающий при постоянном давлении, называетсяизобарным. Из объединенного газового закона для изобарного процесса следует:
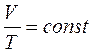 (уравнение изобарного процесса).
(уравнение изобарного процесса).
Процесс, протекающий при постоянном объеме, называется изохорным. Из объединенного газового закона для изохорного процесса следует:
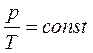 (уравнение изохорного процесса).
(уравнение изохорного процесса).
Процесс, протекающий при постоянной температуре, называется изотермическим. Для изотермического процесса:
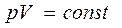 (уравнение изотермического процесса).
(уравнение изотермического процесса).
Идеальный газ.
Простейшей термодинамической системой, рассматриваемой в классической молекулярно-кинетической теории газов, является так называемый идеальный газ. Идеальный газ является важной идеализированной термодинамической системой. Понятие идеального газа играет в термодинамике такую же роль, как и понятия материальной точки и твердого тела в механике. Идеальный газ - это модель, удобная для изучения молекулярных явлений. Из опыта известно, что при достаточном разрежении все газы ведут себя одинаковым образом. Идеализированная система, обладающая свойствами предельно разреженных газов, и представляет собой идеальный газ.
азреженным можно считать такой газ, у которого среднее расстояние между молекулами 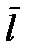 много больше диаметра молекулы
много больше диаметра молекулы 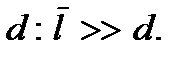 Запишем этот критерий в несколько ином виде. Будем считать, что на каждую молекулу в газе приходится кубик объемом
Запишем этот критерий в несколько ином виде. Будем считать, что на каждую молекулу в газе приходится кубик объемом 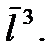 Тогда
Тогда 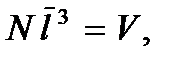 где
где 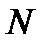 – общее число молекул в газе, или
– общее число молекул в газе, или 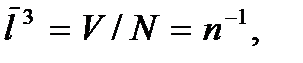 где
где 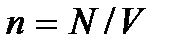 – число молекул в единице объема газа (концентрация молекул газа). Откуда
– число молекул в единице объема газа (концентрация молекул газа). Откуда 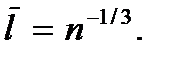 Следовательно, условие разреженности газа можно записать в виде
Следовательно, условие разреженности газа можно записать в виде 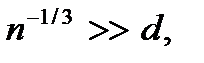 или
или
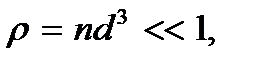 (2.1)
(2.1)
где 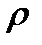 – безразмерный параметр плотности. При таком среднем расстоянии между молекулами силами их взаимодействия можно пренебречь. Взаимодействие молекул происходит только при их непосредственном соприкосновении. Причем это взаимодействие можно рассматривать как взаимодействие твердых непроницаемых шаров. Энергию такого взаимодействия можно представить в виде
– безразмерный параметр плотности. При таком среднем расстоянии между молекулами силами их взаимодействия можно пренебречь. Взаимодействие молекул происходит только при их непосредственном соприкосновении. Причем это взаимодействие можно рассматривать как взаимодействие твердых непроницаемых шаров. Энергию такого взаимодействия можно представить в виде
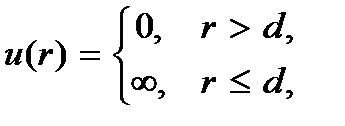
где 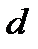 – диаметр молекулы – твердого шара. Зависимость u(r) показана на рис. 2.1. Видим, что при
– диаметр молекулы – твердого шара. Зависимость u(r) показана на рис. 2.1. Видим, что при 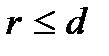 имеет место бесконечно
имеет место бесконечно
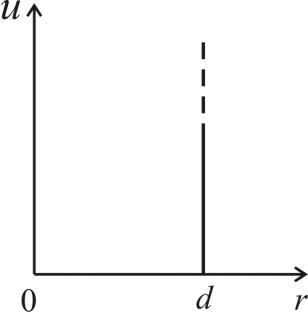 Рис. 2.1 Рис. 2.1
|
высокий потенциальный барьер, препятствующий сближению центров молекул на расстояние, меньшее 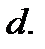 Предполагается также, что в идеальном газе молекулы имеют исчезающе малые собственные размеры, поэтому суммарным объемом молекул по сравнению с объемом, занимаемым газом, можно пренебречь.
Предполагается также, что в идеальном газе молекулы имеют исчезающе малые собственные размеры, поэтому суммарным объемом молекул по сравнению с объемом, занимаемым газом, можно пренебречь.
Модель идеального газа лежит в основе молекулярно-кинетической теории вещества. В молекулярно-кинетической теории волновыми свойствами молекул пренебрегают, каждая молекула рассматривается как классические частицы с достаточно точно определенным положением в пространстве и импульсом. Это оказывается возможным, если среднее расстояние между молекулами много меньше длины волны де Бройля молекулы, т.е. если 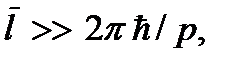 где p = mv – импульс молекулы. Учитывая, что
где p = mv – импульс молекулы. Учитывая, что
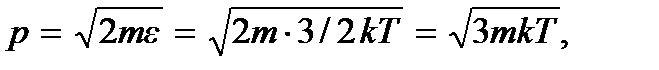
придем к критерию классического идеального газа:
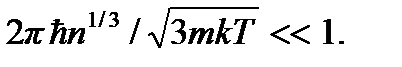
В современной физике понятие идеального газа используется при описании ансамблей любых слабо взаимодействующих частиц. Как видно из вышеприведенного критерия, модель идеального газа справедлива для реальных и квантовых газов при высоких температурах и разрежениях.
Термодинамическое состояние идеального газа характеризуется тремя параметрами – давлением  объемом
объемом 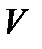 и температурой
и температурой 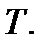 Указанные параметры связаны между собой уравнением, называемым уравнением состояния идеального газа, или уравнением Клапейрона – Менделеева. Это уравнение получено опытным путем и имеет вид
Указанные параметры связаны между собой уравнением, называемым уравнением состояния идеального газа, или уравнением Клапейрона – Менделеева. Это уравнение получено опытным путем и имеет вид
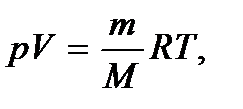 (2.2)
(2.2)
где 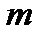 – масса газа,
– масса газа, 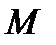 – молярная масса газа,
– молярная масса газа, 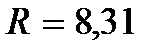 Дж / (моль∙К) – универсальная (молярная) газовая постоянная. Отношение
Дж / (моль∙К) – универсальная (молярная) газовая постоянная. Отношение 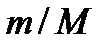 представляет собой число молей (обозначают
представляет собой число молей (обозначают 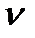 ) в данной массе
) в данной массе 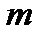 газа. Это же число можно определить как
газа. Это же число можно определить как 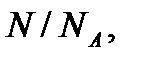 где
где 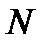 – число молекул в массе
– число молекул в массе 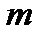 газа. С учетом этого уравнение состояния идеального газа можно переписать в виде
газа. С учетом этого уравнение состояния идеального газа можно переписать в виде
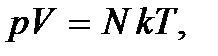 (2.3)
(2.3)
где 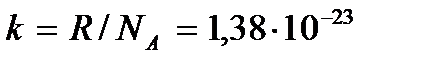 Дж / К – так называемая постоянная Больцмана. Уравнение состояния можно записать и в виде
Дж / К – так называемая постоянная Больцмана. Уравнение состояния можно записать и в виде
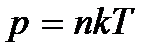 . (2.4)
. (2.4)
Используя это уравнение, критерий идеальности газа (2.1) можно привести к виду 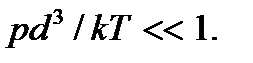 Отсюда видно, что газ тем больше приближается к идеальному, чем меньше его давление и выше температура.
Отсюда видно, что газ тем больше приближается к идеальному, чем меньше его давление и выше температура.
Формула (2.2), записанная для одного моля, может служить определением идеального газа: идеальный газ – это некоторое тело, один моль которого подчиняется уравнению состояния
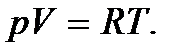
Процессы, при которых один из параметров остается постоянным, называют изопроцессами. Процесс, протекающий при постоянной температуре ( 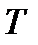 = const), называется изотермическим. При изотермическом процессе давление и объем идеального газа связаны между собой соотношением
= const), называется изотермическим. При изотермическом процессе давление и объем идеального газа связаны между собой соотношением 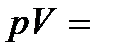 const – закон Бойля – Мариотта. Если при протекании процесса остается постоянным давление (
const – закон Бойля – Мариотта. Если при протекании процесса остается постоянным давление ( 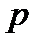 = const), то процесс называется изобарным. При изобарном процессе объем и температура газа связаны соотношением V/T = = const – закон Гей – Люссака. Если неизменным сохраняется объем, процесс называется изохорным (
= const), то процесс называется изобарным. При изобарном процессе объем и температура газа связаны соотношением V/T = = const – закон Гей – Люссака. Если неизменным сохраняется объем, процесс называется изохорным ( 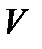 =const). При изохорном процессе давление и температура газа связаны между собой соотношением
=const). При изохорном процессе давление и температура газа связаны между собой соотношением 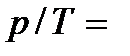 const – закон Шарля. Видим, таким образом, что при изотермическом процессе давление обратно пропорционально объему газа, при изохорном процессе давление прямо пропорционально температуре, а при изобарном процессе объем пропорционален температуре.
const – закон Шарля. Видим, таким образом, что при изотермическом процессе давление обратно пропорционально объему газа, при изохорном процессе давление прямо пропорционально температуре, а при изобарном процессе объем пропорционален температуре.
Закон Максвела
Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dN молекул однородного (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т скорости, заключенные в интервале от v до v + dv.
Для вывода функции распределения молекул по скоростям f(v) равной отношению числа молекул dN, скорости которых лежат в интервале v ÷ v + dv к общему числу молекул N и величине интервала dv
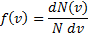
Максвелл использовал два предложения:
а) все направления в пространстве равноправны и поэтому любое направление движения частицы, т.е. любое направление скорости одинаково вероятно. Это свойство иногда называют свойством изотропности функции распределения.
б) движение по трем взаимно перпендикулярным осям независимы т.е. х-компоненты скорости 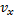 не зависит от того каково значения ее компонент
не зависит от того каково значения ее компонент 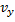 или
или 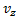 . И тогда вывод f(v) делается сначала для одной компоненты
. И тогда вывод f(v) делается сначала для одной компоненты 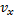 , а затем обобщается на все координаты скорости.
, а затем обобщается на все координаты скорости.
Считается также, что газ состоит из очень большого числа Nтождественных молекул находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Силовые поля на газ не действуют.
Функции f(v) определяет относительное число молекул dN(v)/N скорости которых лежат в интервале от v до v + dv (например: газ имеет N= 106 молекул, при этом dN = 100
молекул имеют скорости от v =100 до v + dv =101 м/с (dv= 1 м 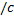 ) тогда
) тогда 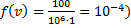 .
.
Используя методы теории вероятностей, Максвелл нашел функцию f(v) -закон распределения молекул идеального газа по скоростям:
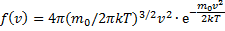
f(v) зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т)
f(v) зависит от отношения кинетической энергии молекулы, отвечающей рассматриваемой скорости 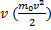 к величине kT характеризующей среднюю тепловую энергию молекул газа.
к величине kT характеризующей среднюю тепловую энергию молекул газа.
 При малых v
При малых v 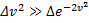 и функция f(v) изменяется практически по параболе
и функция f(v) изменяется практически по параболе 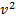 . При возрастании v множитель
. При возрастании v множитель 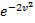 уменьшается быстрее, чем растет множитель
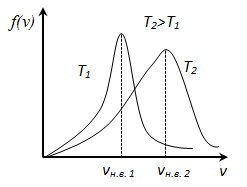
уменьшается быстрее, чем растет множитель 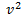 , т.е. имеется max функции f(v). Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью
, т.е. имеется max функции f(v). Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью 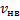 найдем из условия
найдем из условия
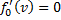
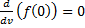
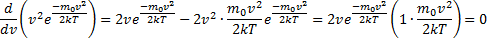
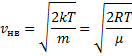
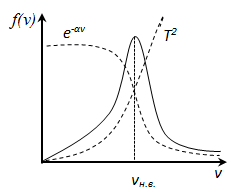
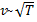 , следовательно, с ростом температуры наиболее вероятная скорость растёт, но площадь S, ограниченная кривой функции распределения остаётся неизменной, так как из условия нормировки
, следовательно, с ростом температуры наиболее вероятная скорость растёт, но площадь S, ограниченная кривой функции распределения остаётся неизменной, так как из условия нормировки 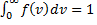 (так как вероятность достоверного события равна 1), поэтому при повышении температуры кривая распределения f(v) будет растягиваться и понижаться.
(так как вероятность достоверного события равна 1), поэтому при повышении температуры кривая распределения f(v) будет растягиваться и понижаться.
 В статистической физике среднее значение какой-либо величины определяется как интеграл от 0 до бесконечности произведения величины на плотность вероятности этой величины (статистический вес)
В статистической физике среднее значение какой-либо величины определяется как интеграл от 0 до бесконечности произведения величины на плотность вероятности этой величины (статистический вес)
<X>= 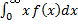
Тогда средняя арифметическая скорость молекул
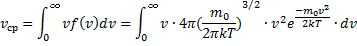
и интегрируя по частям получили
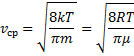
Скорости, характеризующие состояние газа
Дата добавления: 2017-05-18; просмотров: 928;