Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания
[править]Резонанс
Из решения видно, что при частоте вынуждающей силы, равной частоте свободных колебаний, оно не пригодно — возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курса математического анализа известно, что решение в этом случае надо искать в виде: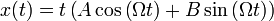 
. Подставим этот анзац в дифференциальное уравнение и получим, что :
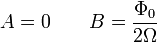
Таким образом, колебания в резонансе будут описываться следующим соотношением:
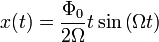
Понятие волны. Продольные и поперечные волны. Энергия бегущей волны. Вектор Умова. Стоячие волны.
Волна называется продольной, если частицы среды совершают колебания в направлении распространения волны (рис. 15.5).
Продольную волну можно наблюдать на длинной мягкой пружине большого диаметра. Ударив по одному из концов пружины, можно заметить, как по пружине будут распространяться последовательные сгущения и разрежения ее витков, бегущие друг за другом. На рисунке 15.6 точками показано положение витков пружины в состоянии покоя, а затем положения витков пружины через последовательные промежутки времени, равные четверти периода.
Таким образом, продольная волна в рассматриваемом случае представляет собой чередующиеся сгущения (Сг) и разрежения (Раз) витков пружины.
Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры
6.Затухающие колебания дифференциальное уравнение
В реальных системах всегда существуют некоторые силы сопротивления, препятствующие развитию колебательных процессов. Для установления характера колебательного движения в этом случае будем считать, что наряду с упругой или квазиупругой силой Fy в системе действует сила трения, пропорциональная скорости и направленная противоположно ей: Fтр =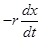 
. Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:
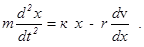8)
Разделив левую и правую части уравнения (8) на m , обозначив r/m = 2bи сохранив обозначение к/m= w02 , приведем это уравнение к виду:
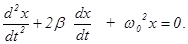(9)
Решение этого уравнения имеет вид:
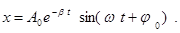(10)
Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы bи w. Коэффициент b = r/2mимеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитудауменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания b. По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний w. Это уменьшение зависит от коэффициента затухания. Оказывается, что
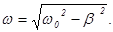(11)
Колебательный процесс может происходить лишь при условии: (w02 - b2)>0, когда частота wв формуле (11) является действительной величиной . Если же затухание в системе слишком велико (w0< b ) , то под корнем в формуле (11) оказывается отрицательная величина, - в этом случае движение не имеет периодического характера.
Графически затухающее колебания представлено на рис.2, где сплошной линией показана зависимость смещения от времени, а пунктирной - экспоненциальный закон убывания амплитуды.
Дата добавления: 2017-05-18; просмотров: 913;