Уравнение Ван-дер-Ваальса примет вид
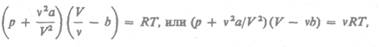
где поправки а и b— постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и V).
При выводе уравнения Ван-дер-Ваальса сделан целый ряд упрощений, поэтому оно также весьма приближенное, хотя и лучше (особенно для несильно сжатых газов) согласуется с опытом, чем уравнение состояния идеального газа.
Уравнение Ван-дер-Ваальса неединственное уравнение, описывающее реальные газы. Существуют и другиеуравнения, некоторые из них даже точнее описывают реальные газы, но не рассматриваются из-за их сложности.
§ 62. ИзотермыВан-дер-Ваальса и их анализ
Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса — кривые зависимости р от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса (61.2) для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис. 89) имеют довольно своеобразный характер. При высоких температурах (T > Tk) изотерма реального газа отличается от изотермы идеального
газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре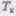 
на изотерме имеется лишь одна точка перегиба К.
Эта изотерма называется критической, соответствующая ей температура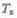 
— критической температурой; точка перегиба К называется критической точкой; в этой точке { касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем 
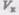и .цишин Pkназываются также критическими. Состояние с критическими парамет-
рами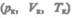 
называется критическим состоянием. При низких температурах
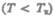изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз,
Дата добавления: 2017-04-20; просмотров: 372;