Уравнение неразрывности

Движение жидкостей называется течением, а совокупность частиц движущейся жид­кости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.

Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

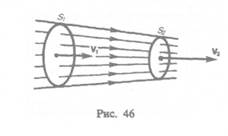
Рассмотрим какую-либо трубку тока. Выберем два ее сечения 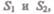перпен-

дикулярные направлению скорости (рис. 46).

За время 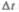через сечение S проходит объем жидкости следовательно, за 1 с

через 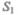пройдет объем жидкости 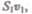где — скорость течения жидкости в месте

сечения 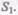Через сечение 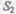за 1 с пройдет объем жидкости 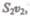где 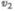— скорость

течения жидкости в месте сечения 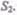Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема то через сечениет

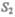
такой же объем жидкости, как и через сечени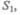е т. е.

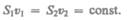(29.1)

Следовательно, произведение скорости течения несжимаемой жидкости на попереч­ное сечение трубки тока есть величина постоянная для данной трубки тока. Соотноше­ние (29.1) называется уравнением неразрывности для несжимаемой жидкости.

§ 30. УравнениеБернулли и следствия из него

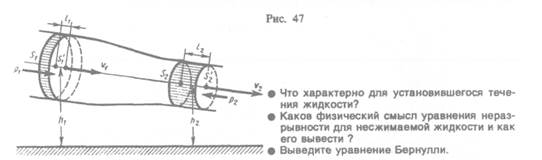
Выделим в стационарно текущей идеальной жидкости (физическая абстракция, т. е. воображаемая жидкость, в которой отсутствуют силы внутреннего трения) трубку тока, ограниченную сечениям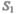и и 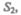по которой слева направо течет жидкость (рис. 47). Пусть в месте сечения 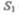скорость течения , давление и высота, на которой это сечение расположено, 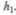Аналогично, в месте сечения 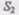скорость течения , давление 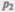и высота сечения 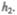За малый промежуток времени At жидкость перемеща­ется от сечения 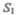к сечению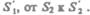

Согласно закону сохранения энергии, изменение полной энергии 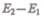идеальной

несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы т жидкости:

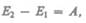(30.1)

где 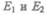— полные энергии жидкости массой т в местах сеченийсоответст­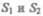

Венно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями 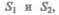за рассматриваемый малый промежуток

времени 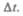Для перенесения массы т от 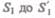жидкость должна переместиться на

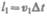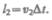расстояние и от — на расстояние Отметим, что 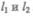настоль-

ко малы, что всем точкам объемов, закрашенных на рис. 47, приписывают постоянные значения скорости давления р и высоты h. Следовательно,

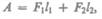(30.2)

где 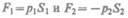(отрицательна, так как направлена в сторону, противополож-

ную течению жидкости; рис. 47).

Полные энергии 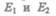будут складываться из кинетической и потенциальной

энергий массы т жидкости:

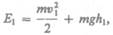(30.3)

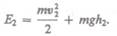(30.4) Подставляя (30.3) и (30.4) в (30.1) и приравнивая (30.1) и (30.2), получим

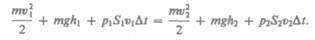(30.5)