Оценка текущей стоимости облигаций

Облигация с нулевым купоном (с дисконтом)- это облигация, по ко­торой текущий доход не выплачивается; облигация продается по цене ни­же номинала, а погашается по номиналу. Текущая стоимость такой обли­гации определяется по формуле:

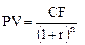(5.17)

где: PV - текущая стоимость облигации, д.е.;

CF - сумма, выплачиваемая при погашении облигации, д.е.;

г - требуемая инвестором ставка дохода в долях единицы;

n - число лет, по истечении которых произойдет погашение об­лигации.

Купоннойназывается облигация, по которой текущий (купонный) до­ход выплачивается с определенной периодичностью (по кварталам, полу­годиям, раз в год). Текущая стоимость купонной облигации рассчитывает­ся по формуле:

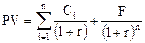(5.18)

где PV - текущая стоимость облигации, д.е.;

С_i - годовой текущий доход в виде процента, выплачиваемый по облигации в i-том периоде, д.е.;

F - сумма, выплачиваемая при погашении, д.е.;

г - требуемая инвестором ставка дохода, коэфф.;

n - число лет, по истечении которых произойдет погашение об­лигации.

Из приведенных формул и расчетов можно сделать ряд выводов.

1. Если купонная ставка совпадает с рыночной ставкой дохода, то тео­ретическая оценка облигации совпадает с номинальной ценой.

2. В случае, когда рыночная ставка выше, чем купонная ставка, теку­щая стоимость облигации становится ниже номинала. В этом случае го­ворят, что облигация продается с дисконтом.

3. В случае, когда рыночная ставка ниже, чем купонная ставка, теку­щая стоимость облигации становится выше номинала. В этом случае го­ворят, что облигация продается с премией (ажио).

4. Если облигация приобретена по номиналу, то ее текущая доходность и доходность до погашения идентична купонной.

5. Если облигация приобретена по цене ниже номинала, то ее текущая доходность и доходность до погашения выше купонной.

6. Если облигация приобретена по цене выше номинала (с премией), то ее текущая доходность и доходность до погашения ниже купонной.