Уравнение прямолинейной регрессии
Корреляционную связь в форме, близкой к прямолинейной, можно представить в виде уравнения прямой линии:
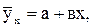 (11.8)
(11.8)
где 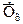 – среднее значение результативного признака; х – значение факторного признака;
– среднее значение результативного признака; х – значение факторного признака; 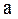 – параметр уравнения, обычно характеризующий минимальное значение результативного признака;
– параметр уравнения, обычно характеризующий минимальное значение результативного признака; 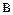 – коэффициент пропорциональности изменения признака-результата.
– коэффициент пропорциональности изменения признака-результата.
В уравнении 9.8 параметр 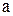 характеризует среднее значение результативного признака у при элиминировании признака-фактора х, т.е. х=0. Коэффициент в зависимости от знака (+) или (–) показывает пропорциональность изменения результата у, т.е. его приращения или убывания при абсолютном изменении фактора на каждую его единицу.
характеризует среднее значение результативного признака у при элиминировании признака-фактора х, т.е. х=0. Коэффициент в зависимости от знака (+) или (–) показывает пропорциональность изменения результата у, т.е. его приращения или убывания при абсолютном изменении фактора на каждую его единицу.
Для нахождения параметров 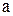 ,
, 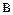 уравнения 9.8 составляют и решают следующую систему нормальных уравнений:
уравнения 9.8 составляют и решают следующую систему нормальных уравнений:
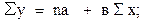 (11.9)
(11.9)
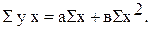 (11.10)
(11.10)
При расчете искомых параметров 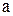 ,
, 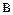 можно воспользоваться макетом табл. 11.5.
можно воспользоваться макетом табл. 11.5.
Т а б л и ц а 11.5. Вспомогательные расчеты для определения параметров уравнения прямолинейной связи
| № п.п. | х | у | х2 | ху |
| х1 | у1 | 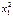
| 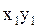
| |
| х2 | у2 | 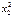
| 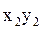
| |
| … | … | … | … | … |
| n | хn | уn | 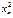
| 
|
| Σ | Σх | Σу | Σх2 | Σху |
Таким образом, для решения системы нормальных уравнений (11.9 и 11.10) необходимо найти значения Σх, Σу, Σху и Σх2.
Допустим, необходимо определить, как изменяется в среднем урожайность рапса в зависимости от колебания доз минеральных удобрений по данным статистической совокупности из 30 сельскохозяйственных организаций, если известно, что дозы удобрений колеблются в пределах от 56 до 183 кг действующего вещества на 1 га, а урожайность рапса – от 16,9 до 30,4 ц/га.
Для составления уравнения прямолинейной регрессии (11.8) по имеющимся данным необходимо решить систему нормальных уравнений. С этой целью прежде всего составим рабочую табл. 11.6.
Т а б л и ц а 11.6. Вспомогательные расчеты для определения параметров уравнения прямолинейной взаимосвязи
| № п.п. | Дозы удобрений, кг/га | Урожайность рапса, ц/га | Произведение вариант | Квадрат доз удобрений |
| х | у | ху | х2 | |
| 16,9 | ||||
| 17,2 | ||||
| … | … | … | … | … |
| 30,4 | ||||
| Σ |
Подставим полученные в табл. 11.6 конкретные значения Σх=3283, Σу=640, Σху=91204 и Σх2=535692 в уравнения 11.9 и 11.10; получим:
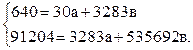
Для расчета коэффициента пропорциональности 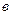 разделим уравнения 1,2 на числа, находящиеся при
разделим уравнения 1,2 на числа, находящиеся при 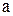 . Получим:
. Получим:
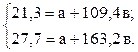
Вычтем четвертое уравнение из третьего. Получим 21,3 – 27,7 = а+а+109,4в – 163,2 в; - 6,4 = - 53,8 в; в = 0,12.
Теперь найдем параметр а, подставив значение в, например, в третье уравнение: 21,3 = а + 109,4. · 0,12; а=8,2.
Уравнение прямолинейной регрессии, выражающее зависимость между дозами минеральных удобрений и урожайностью рапса, имеет следующий вид:
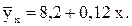 (11.11)
(11.11)
Коэффициент пропорциональности в показывает, что повышение доз внесения в почву минеральных удобрений на 1 кг действующего вещества может вызвать прирост урожайности рапса в сельскохозяйственных организациях 12 кг. Это свидетельствует о существенной роли минеральных туков в достижении высоких и устойчивых урожаев сельскохозяйственных культур.
Дата добавления: 2017-04-20; просмотров: 464;
