Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между 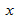 и
и 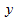 нет линейного соотношения: изменение
нет линейного соотношения: изменение 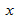 не влияет на
не влияет на 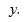
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент 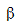 равен нулю можно воспользоваться следующим алгоритмом:
равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению 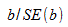 , которая подчиняется
, которая подчиняется 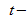 распределению с
распределению с 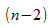 степенями свободы, где
степенями свободы, где 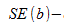 стандартная ошибка коэффициента
стандартная ошибка коэффициента 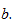
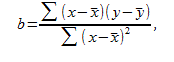
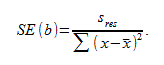 ,
,
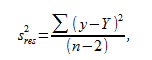 - оценка дисперсии остатков.
- оценка дисперсии остатков.
Обычно если достигнутый уровень значимости 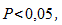 нулевая гипотеза отклоняется.
нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента 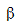 :
:
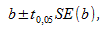
где 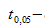 процентная точка
процентная точка 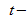 распределения со степенями свободы
распределения со степенями свободы 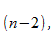 что дает вероятность двустороннего критерия
что дает вероятность двустороннего критерия 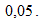
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, 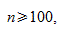 мы можем аппроксимировать
мы можем аппроксимировать 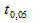 значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
24. Построение линейной корреляции.
Корреляционная зависимость между случайными величинами Х и У называется линейной корреляцией, если обе функции регрессии f(y) и g(x) являются линейными. В этом случае линии регрессии- прямые и называются прямыми регрессии.
Выведем уравнение прямой регрессии У на Х, т.е. найдем коэффициенты линейной функции g(x) = AX +B.
Введем обозначения М(Х) =а, М(У) =b, D(X) =s12, D(Y) ==s22, М(ХУ) – М(Х)М(У) = m .
Используем свойства математического ожидания:
М(У) =М(g(x))= M(AX +B) = AM(X) +B, тогда B = b – Aa.
M(XY) = M(Xg(x)) = M(AX 2 + BX ) = AM(X2) + BM(X) AM(X2) + (b – Aa)a, откуда
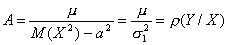
- называется коэффициентом регрессии У на Х. Уравнение прямой регрессии У на Х имеет вид :
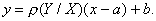
Аналогично получим уравнение прямой регрессии Х на У :
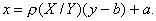
Выразим коэффициенты регрессии через коэффициент корреляции:
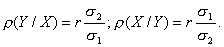
 Тогда уравнения примут вид:
Тогда уравнения примут вид:
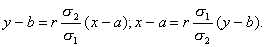
Обе прямые проходят через общую точку (a; b) , угловые коэффициенты прямых регрессии равны:
для прямой регрессии У на Х -
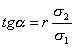
для прямой регрессии Х на У -
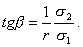
Чем ближе | r | к единице, тем меньше угол между прямыми регрессии, и только в случае | r | =1 прямые сливаются.
Коэффициент корреляции связан с коэффициентами регрессии соотношением:
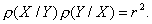
25. Оценки числовых характеристик генеральной совокупности.
Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.
Точечной оценкой генеральной средней является выборочное среднее 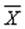 .
.
Выборочным средним называется среднее арифметическое значение признака выборочной совокупности.
Если все значения x1, x2,..., xn признака выборки различны (или если данные не сгруппированы), то:
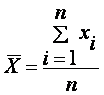
Если же все значения признака x1, x2,..., xn имеют соответственно частоты n1, n2,..., nk, причем n1 + n2 +...+ nk = n (или если выборочное среднее вычисляется по вариационному ряду), то
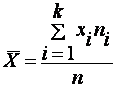
В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего 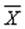 значениями вариант считают середины интервалов.
значениями вариант считают середины интервалов.
Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0).
Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.
Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году.
Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 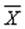 .
.
Если все значения x1, x2,..., xn признака выборки объема n различны, то:
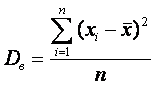
Если же все значения признака x1, x2,..., xn имеют соответственно частоты n1, n2,..., nk, причем n1 + n2 +...+ nk = n, то
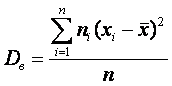
Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.
Среднее квадратическое отклонение (стандартное отклонение), (от английского standard deviation) вычисляется как корень квадратный из дисперсии.

Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.
Непараметрическими характеристиками положения являются мода и медиана.
Модой Mo называется варианта, имеющая наибольшую частоту или относительную частоту.
Медианой Me называется варианта, которая делит вариационный ряд на две части, равные по числу вариант.
При нечетном числе вариант (n=2k+1)
Me = xk+1,
а при четном числе вариант (n=2k)
Me = (xk + xk+1)/2.
26. Статистические гипотезы.
Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Выдвигается основная (нулевая) гипотеза 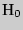 и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу
и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу  , которая противоречит нулевой.
, которая противоречит нулевой.
В результате статистической проверки гипотезы могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза; вероятность совершить такую ошибку обозначают 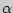 и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают
и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают 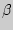 , а мощностью критерия является вероятность
, а мощностью критерия является вероятность 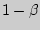 .
.
Процедура обоснованного сопоставления высказанной гипотезы с имеющейся выборкой осуществляется с помощью того или иного статистического критерия и называется статистической проверкой гипотез. Под критической областью понимают совокупность значений критерия, при которых нулевую гипотезу 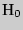 отвергают. Критическую область при заданном уровне значимости следует строить так, чтобы мощность критерия была максимальной.
отвергают. Критическую область при заданном уровне значимости следует строить так, чтобы мощность критерия была максимальной.
Статистические критерии проверки гипотез разнообразны, но у них единая логическая схема построения, которую представим на рис. 103.
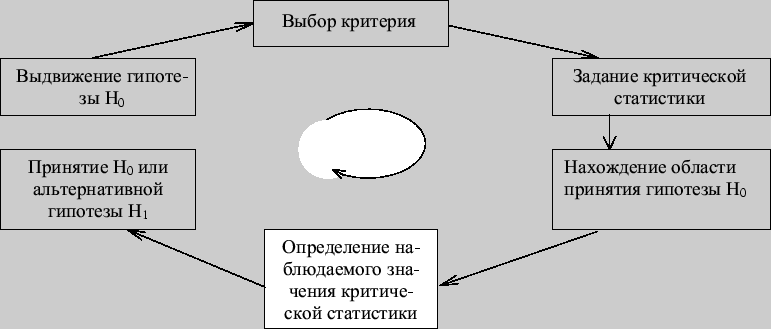
Рис. 103
27. Статистические критерии оценки гипотез.
1. Сравнение двух дисперсий нормальных генеральных совокупностей. При заданном уровне значимости 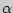 проверяется нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:
проверяется нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:
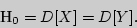
В качестве критерия проверки нулевой гипотезы принимают случайную величину отношения большей исправленной дисперсии к меньшей
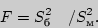
Величина 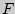 имеет распределение Фишера-Снедекора, которое зависит только от чисел степеней свободы
имеет распределение Фишера-Снедекора, которое зависит только от чисел степеней свободы 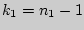 и
и 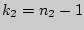 .
.
2. Сравнение двух средних нормальных генеральных совокупностей с известными дисперсиями.Проверяется нулевая гипотеза о равенстве генеральных средних рассматриваемых совокупностей с заданными или вычисляемыми дисперсиями. В качестве критерия проверки нулевой гипотезы примем случайную величину
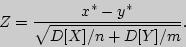
3. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности.По выборочной средней при заданном уровне значимости проверяется нулевая гипотеза 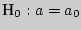 о равенстве генеральной средней
о равенстве генеральной средней 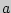 гипотетическому значению
гипотетическому значению 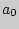 . В качестве проверки нулевой гипотезы примем случайную величину
. В качестве проверки нулевой гипотезы примем случайную величину
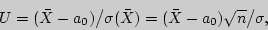
которая распределена нормально.
4. Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события.При заданном уровне значимости 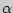 проверяется нулевая гипотеза, состоящая в том, что неизвестная вероятность
проверяется нулевая гипотеза, состоящая в том, что неизвестная вероятность  появления события равна гипотетической вероятности
появления события равна гипотетической вероятности 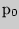 серии повторных независимых испытаний.
серии повторных независимых испытаний.
В качестве критерия проверки нулевой гипотезы принимаем случайную величину
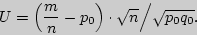
Дата добавления: 2017-04-20; просмотров: 2263;
