Модели стационарных и нестационарных временных рядов и их идентификация

Модели авторегрессии порядка p (AutoRegressive - AR(p) models).

Достаточно часто экономические показатели, представленные в виде временного ряда, имеют сложную структуру. Моделирование таких рядов путем построения модели тренда, сезонности и периодической составляющей не приводит к удовлетворительным результатам. Ряд остатков часто имеет статистические закономерности. Наиболее распространенными моделями стационарных рядов являются модели авторегрессии и модели скользящего среднего.

Будем рассматривать класс стационарных временных рядов. Задача состоит в построении модели остатков временного ряда u_t и прогнозирования его значений.

Авторегрессионная модель предназначена для описания стационарных временных рядов. Стационарный процесс удовлетворяет уравнению авторегрессии бесконечного порядка с достаточно быстро убывающими коэффициентами. В частности поэтому авторегрессионная модель достаточно высокого порядка может хорошо аппроксимировать почти любой стационарный процесс. В связи с этим модель авторегрессии часто применяется для моделирования остатков в той или иной параметрической модели, например регрессионной модели или модели тренда.

Модель авторегрессии порядка 1 AR(1) (марковский процесс).

Марковскими называются процессы, в которых состояние объекта в каждый следующий момент времени определяется только состоянием в настоящий момент и не зависит от того, каким путем объект достиг этого состояния. В терминах корреляционного анализа для временных рядов марковский процесс можно описать следующим образом: существует статистически значимая корреляционная связь исходного ряда с рядом, сдвинутым на один временной интервал, и отсутствует с рядами, сдвинутыми на два, три и т. д. временных интервала. В идеальном случае эти коэффициенты корреляции равны нулю.

Авторегрессионная модель первого порядка определяется соотношением:

u(t)=m u(t-1)+e(t) , (5.1)

где m - числовой коэффициент |m|<1, e(t) – последовательность случайных величин, образующих «белый шум» (E(e(t))=0, E(e(t)e(t+t))= ).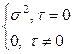

Модель (5.1) называется также марковским процессом.

Имеем:

E(u(t))º0. (5.2)

r(u(t)u(t±t))=m^t. (5.3)

Du(t)=s²/(1-m²). (5.4)

cov(u(t)u(t±t))=m^tDu(t). (5.5)

Из (5.3) следует, что при |m| близком к единице дисперсия u(t) будет намного больше дисперсии e_t. Это значит (учитывая (5.2) m=r(u(t)u(t±1))=r(1), т.е. параметр m может быть интерпретирован как значение автокорреляции первого порядка), что в случае сильной корреляции соседних значений ряда u(t) ряд слабых возмущений e_t будет порождать размашистые колебания остатков u(t).

Условие стационарности ряда (5.1) определяется требованием |m|<1.

Автокорреляционная функция (АКФ) r(t) марковского процесса определяется соотношением (5.3).

Частная автокорреляционная функция

r_част(t)=r(u(t)u(t+t)) | u(t+1)=u(t+2)=…=u(t+t-1)=0

может быть вычислена по формуле: r_част(2)=(r(2)-r²(1))/(1-r²(1)). Для второго и выше порядков (см. [1], с. 413, 414) должно быть r_част(t)=0 "t=2,3,… . Это удобно использовать для подбора модели (5.1): если вычисленные по оцененным невязкам u(t)=y_t- 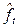выборочные частные корреляции статистически незначимо отличаются от нуля при t=2,3,…, то использование модели AR(1) для описания случайных остатков не противоречит исходным данным.

Идентификация модели. Требуется статистически оценить параметры m и s² модели (5.1) по имеющимся значениям исходного ряда y_t.

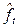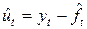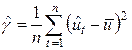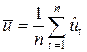Выделяем неслучайную составляющую и получаем невязки . Находим дисперсию невязок , где (для большинства методов выделения 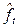автоматически 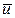=0). Далее с учетом (5.2), (5.3) получим формулы для оценки параметров модели (5.1):

,

.

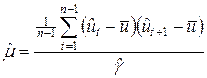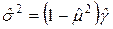Модели авторегрессии р порядка – AR(p) при p³2 см. в [1], с. 834-837:

u(t)=m₁u(t-1)+m₂u(t-2)+…+e(t). (5.6)

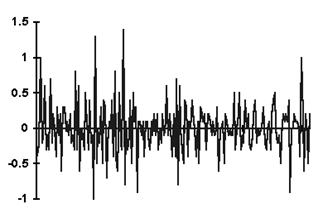
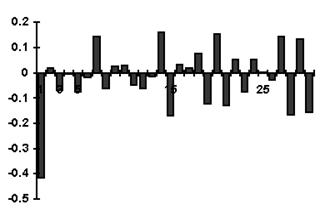
Пример. График первой разности ряда, хорошо описывающейся моделью AR(1), представлен на рис. 5.1; график выборочной автокорреляционной функции (АКФ) первой разности этого ряда представлен на рис. 5.2. Ñ

Рис. 5.1	Рис. 5.2

Модели скользящего среднего порядка q (Moving Average - MA(q) models).

Часто на показатель в текущий момент времени оказывает воздействие значение показателя в предыдущие моменты. Хотя воздействие отдаленных элементов незначительно, в сумме оно может оказывать существенное влияние на модель. Учесть это воздействие возможно в модели скользящего среднего. Моделирование воздействия всех предшествующих элементов ряда на показатель в текущий момент основано на предпосылке о том, что в ошибках модели за несколько предшествующих периодов сосредоточена информация о всей предыстории ряда.

Моделью скользящего среднего порядка q называется процесс:

u(t)=e(t)-q₁e(t-1)-q₂e(t-2)-…-q_qe(t-q). (5.7)

В частности, модели порядка 1 и 2 соответственно имеют вид:

u(t)=e(t)-qe(t-1), (5.8)

u(t)=e(t)-q₁e(t-1)-q₂e(t-2). (5.9)

Переход от формы (5.6) к форме (5.7) осуществляется с помощью последовательной подстановки в правую часть формулы (5.6) вместо u(t-1), u(t-2), … их выражений, вычисленных по формуле (5.6) для моментов времени t-1, t-2, …. Это означает двойственность в представлении анализируемого временного ряда – две эквивалентные формы линейного процесса - и обратимость AR и MA моделей.

В качестве примера рассмотрим модель скользящего среднего первого порядка – МА(1). Данная модель описывается соотношением (5.8). Можно показать, что стационарность u(t) обеспечивается при любом значении параметра q. Модель обратима (представима в виде модели авторегрессии бесконечного порядка) при условии |q|<1.

Автокорреляционная функция:

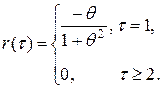
Частная корреляционная функция процесса МА(1), определяющая степень тесноты корреляционной связи между u(t) и u(t±t), t=1,2, … при фиксированных значениях всех промежуточных элементов этого ряда задается выражением:

.

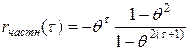Идентификация модели МА(1). Требуется статистически оценить параметры q и s² модели (5.8) по имеющимся значениям исходного ряда y_t. Выделяем неслучайную составляющую 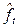и получаем невязки 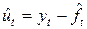. Находим оценку автокорреляции :

.

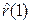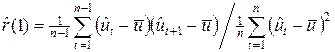Подставляя 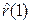в выражение для автокорреляционной функции, имеем квадратное уравнение для q:

q²+(1/ 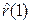)q+1=0.

Из двух решений приведенного квадратного уравнения (q₁q₂=1) одно будет меньше единицы – его и выбираем в качестве искомой оценки параметра в модели МА(1).

Оценка s² получается по формуле: .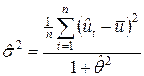

Модель скользящего среднего второго порядка – МА(2) отличается более сложным построением -см. [1], с. 843-845.

Важное практическое значение имеют процессы, первая (или более высокая) разность которых стационарна и является процессом МА(q). Подобные процессы устроены как случайные колебания с непостоянным средним уровнем, или (для второй разности) непостоянным углом наклона.

Модели авторегрессии-скользящего среднего (AutoRegressive - Moving Average - ARMA(р, q) models).

На практике для экономичной параметризации анализируемого процесса иногда бывает необходимо включить в модель как члены, описывающие авторегрессию, так и члены, моделирующие остаток в виде скользящего среднего. Такой линейный процесс имеет вид:

u(t)=m₁u(t-1)+…+m_рu(t-р)+e(t)-q₁e(t-1)-…-q_qe(t-q) (5.10)

и называется процессом авторегрессии - скользящего среднего порядка (p, q) – ARMA(p, q).

Рассмотрим в качестве примера модель ARMA(1,1). В соответствии с моделью (5.10) процесс ARMA(1, 1) описывается формулой:

u(t)=mu(t-1)+e(t)-qe(t-1) или u(t)-mu(t-1)=e(t)-qe(t-1).

Процесс ARMA(1, 1) стационарен, если корень характеристического уравнения AR(1) модели 1-mz=0 по модулю больше единицы. То есть должно быть |m|<1. Обратимость процесса ARMA(1, 1) обеспечивается требованием, чтобы корень характеристического уравнения МA(1) модели 1-qz=0 по модулю был больше единицы. То есть должно быть |q|<1. АКФ:

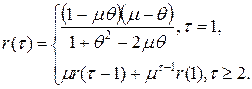
Автокорреляционная функция экспоненциально убывает от начального значения r(1), причем это убывание монотонно, если m положительно, и колебательно (знакопеременно), если m отрицательно.

Из последнего равенства и условий стационарности и обратимости следует, что r(1) и r(2) должны удовлетворять условиям:

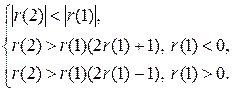
Эти условия бывают полезными при проверке гипотезы (по выборочным значениям коэффициентов автокорреляции) о том, что анализируемый процесс может быть описан ARMA(1, 1) моделью.

Идентификация модели ARMA(1, 1). Требуется статистически оценить параметры m, q и s² модели по имеющимся значениям исходного ряда y_t.

Этап 1.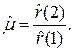

Этап 2. Из уравнения модели несложно получить систему уравнений вида:

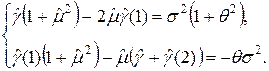
Поделив первое уравнение системы на второе, получим квадратное уравнение относительно q:

A=-(1+q²)/q, где А=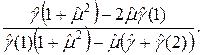

Из двух корней уравнения выбираем тот, который удовлетворяет условию обратимости |q|<1. Оценку s² определяем из любого уравнения системы.

Модель авторегрессии - проинтегрированного скользящего среднего (AutoRegressive Integrated Moving Average - ARIMA(р, q, k) models).

Модель впервые была предложена Дж.Боксом и Г.Дженкинсом и поэтому известна как модель Бокса-Дженкинса. Это одна из наиболее популярных моделей для построения краткосрочных прогнозов значений временных рядов.

Будем рассматривать нестационарные, однородные временные ряды. То есть ряды, для которых случайный остаток u(t), получающийся после вычитания из ряда y(t) его неслучайной составляющей f(t), представляет нестационарный временной ряд. Модель Бокса-Дженкинса предназначена для описания нестационарных временных рядов со следующими свойствами:

а) в рамках аддитивной модели y(t) включает f(t), имеющий вид алгебраического полинома от t степени k-1, причем коэффициенты полинома могут быть как стохастические, так и нестохастические,

б) ряд y_k(t), t=1,2,…, n-k, получившийся из y(t) после применения к нему метода последовательных разностей, может быть описан моделью ARMA(р, q).

Следовательно, модель Бокса-Дженкинса имеет вид:

y_k(t)=m₁y_k(t-1)+…+m_рy_k(t-р)+e(t)-q₁e(t-1)-…-q_qe(t-q), (5.11)

где y_k(t)=D^ky(t)=y(t)-C_k¹y(t-1)+C_k²y(t-2)-…+(-1)^ky(t-k), t=k+1, k+2, …, n. Здесь D^k – k-я последовательная разность анализируемого процесса y(t) (D=y(t)-y(t-1), D²=Dy(t)-Dy(t-1) и т.п.).

Введем операторы сдвига во времени:

F₊y_t=y_t+1 и F_-y_t=y_t-1.

Причем F₊F_-=1, F^k_-y_t=y_t-k, F^k₊y_t=y_t+k, D=1-F_- .

Тогда оператор авторегрессии порядка p AR(p) имеет вид:

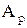(F_-, m)=1-m₁F_--m₂F²_-- … -m_pF^p_- ,

а оператор скользящего среднего порядка q MA(q):

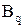(F_-, q)=1-q₁F_--q₂F²_-- … -q_qF^q_{- .}

Модель ARIMA(р, q, k) будет с учетом формулы (5.11) и введенных операторов иметь вид:

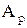(F_-, m)D^ky(t)= 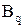(F_-, q)e(t). (5.11^а)

На практике применяются модели ARIMA(р, q, k), в которых р, q, k не превышают 2. Например, ARIMA(1, 1, 1):

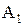(F_-, m)Dy(t)= 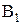(F_-, q)e(t) Þ (1-mF_-)(y_t-y_t-1)=(1-qF_-)e_t Þ

y_t-y_t-1-my_t-1+my_t-2=e_t-qe_t-1 Þ

y(t)=(1+m)y(t-1)-my(t-2)+e(t)-qe(t-1).

Частным случаем модели ARIMA является модель авторегрессии АR(p), для которой q=k=0. Другой частный случай - модель скользящего среднего MA(q), для которой p=k=0.

Важные специальные классы моделей - модели ARIMA(0, q, k), и модели ARMA(p, q) = ARIMA(р, q, 0).

Модель АR(1) при положительном коэффициенте автокорреляции представляет собой колебательный процесс с преобладанием длинных волн. Если коэффициент корреляции отрицателен, процесс является сильно осциллирующим. Модель ARIMA(0, 1, 1) описывает случайный процесс с непостоянным уровнем. Аналогичное утверждение справедливо для модели ARIMA(0, 2, 2), описывающей случайный процесс с переменным уровнем и углом наклона.

Идентификация ARIMA моделей.

Структура модели ARIMA описывается тремя параметрами (р, q, k). Кроме того, разные по форме модели могут быть довольно близки друг другу. Поэтому весьма важно по возможности правильно определить структуру модели. Рассмотрим этапы идентификации.

1. Подбирается порядок модели k. Для этого используется либо метод последовательных разностей, либо анализ автокорреляционных функций процессов Dy(t), D²y(t), … - пока не достигнем быстрого затухания (стационарности) автокорреляционной функции для некоторого k. Дж.Бокс и Г.Дженкинс предлагают взять за визуальный критерий стационарности быстрое убывание значений выборочной АКФ. Использование завышенного порядка разности приводит к росту дисперсии ошибок и к заметному росту дисперсии прогноза.

2. Находим y_k(t)=D^ky(t) и идентифицируем ARMA(р, q) модель.

Пример. Для определения порядков авторегрессии и скользящего среднего продемонстрируем вид и свойства теоретических АКФ и частной АКФ простейших моделей.

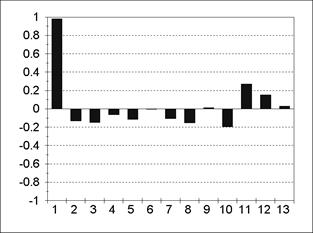
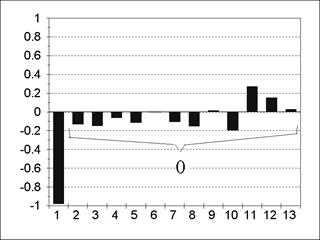
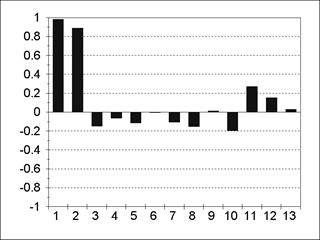
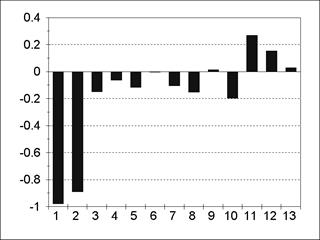
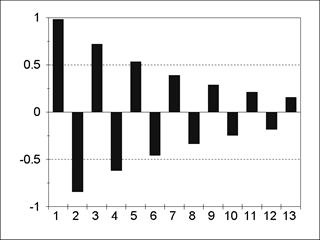
Пример АКФ и частной АКФ для модели АR(1) представлен на рис. 5.3; 5.4. Пример АКФ и частной АКФ для модели АR(2) содержится на рис. 5.5; 5.6. Из содержания рис. 5.3-5.6 следует, что все значения частной АКФ для лагов, больших порядка авторегрессии, статистически незначимы. Пример АКФ и частной АКФ для модели MА(1) изображен на рис. 5.7; 5.8.

Рис. 5.3	Рис. 5.4
Рис. 5.5	Рис. 5.6
Рис. 5.7.	Рис. 5.8.

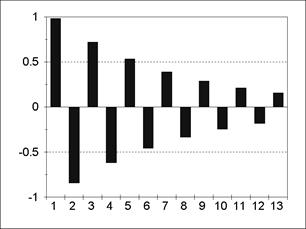
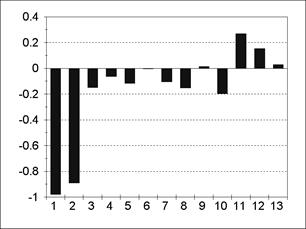
Пример АКФ и частной АКФ для модели MА(2) представлен на рис. 5.9; 5.10. Для модели MА(q) все значения АКФ для лагов, больших q, равны нулю. Для модели ARMA(р, q) значения АКФ после лага p-q представляют собой смесь затухающих синусоид и экспонент, а значения частной АКФ ведут себя аналогично после лага q-p. Ñ

Рис. 5.9	Рис. 5.10

Общий подход Бокса-Дженкинса к анализу временных рядов показан на рис. 5.11. Схема процесса выбора модели временного ряда показана на рис. 5.12.

Если процесс выбора модели успешно осуществлен, возникает проблема оценки качества построенной модели. Для «хорошей» модели остатки должны быть «белым шумом», т.е. их выборочные автокорреляции не должны значимо отклоняться от нуля. Кроме того, модель не должна содержать лишних параметров, т.е. нельзя уменьшить число параметров без появления значимой автокорреляции остатков. Для диагностики модели необходимо попытаться модифицировать ее, меняя порядки авторегрессии и скользящего среднего. Одновременно повышать оба порядка не рекомендуется ввиду опасности вырождения модели.