Динамика предельного дохода в условиях чистой монополии
| Цена (Р), (у.е.) | Объем (Q), шт. | Совокупный доход (TR), у.е. | Предельный доход на единицу выпуска (MR), y.e. |
Государственная монополия- базируется на исключительном праве государства, например, на регулирование и предложение денег, производство некоторых общественных товаров, покупку вооружения и т.п.
Временная монополия – порождение НТП, возникает на основе монопольного обладания фирмой патентами, лицензиями на какое – либо научно- техническое достижение.
Случайная монополия – результат ограниченного во времени превышения спроса над предложением, позволяющих продавцу повышать цены.
5. ВЫБОР ОПТИМАЛЬНОГО ОБЪЕМА ПРОИЗВОДСТВА
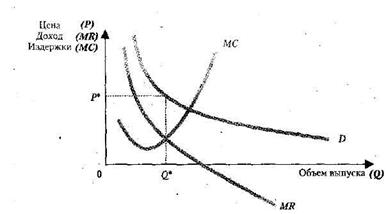
Предположим, что структура издержек фирмы-монополиста задана кривыми АТС, МС, ТС, а предельный доход определяется кривой спроса. Сколько продукции следует произвести фирме-монополисту?
Необходимым условием максимизации прибыли, как было уже рассмотрено ранее, является равенство предельного дохода и предельных издержек:
МС = MR.
Если предельные издержки превышают величину предельного дохода (МС > MR), то монополист может увеличить прибыль за счет сокращения объема производства. И наоборот, если предельные издержки меньше предельного дохода (МС < MR), объем совокупной прибыли может быть увеличен за счет расширения производства. Лишь при равенстве рассматриваемых показателей в точке Q* достигается оптимальный объем производства (рис. 8.2).
Достаточным условием максимизации прибыли, а не условием минимизации прибыли является условие второго порядка (см. математическое приложение):
n"(Q)= TR"(Q) - TC"(Q)<0
или MR'(Q) - MC'(Q) < 0.
Это означает, что кривая предельного дохода пересекает кривую предельных издержек сверху вниз (рис. 5).
|
|
Рис. 5. Оптимальный объем выпуска монополиста
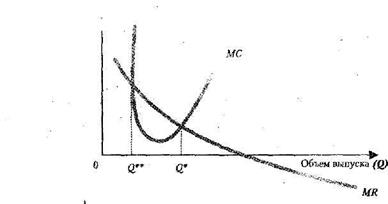
Рис.6. Условия минимизации прибыли
В противном случае равенство MR = МС обеспечивало бы в точке Q** минимизацию прибыли (рис. 6).
Задача 1
Дата добавления: 2017-01-29; просмотров: 636;
